Kolmogorov-Smirnov Test in R Programming

The Kolmogorov-Smirnov Test is a type of non-parametric test of the equality of discontinuous and continuous a 1D probability distribution that is used to compare the sample with the reference probability test (known as one-sample K-S Test) or among two samples (known as two-sample K-S test). A K-S Test quantifies the distance between the cumulative distribution function of the given reference distribution and the empirical distributions of given two samples, or between the empirical distribution of given two samples. In a one-sample K-S test, the distribution that is considered under a null hypothesis can be purely discrete or continuous, or mixed. In the two-sample K-S test, the distribution considered under the null hypothesis is generally continuous distribution but it is unrestricted otherwise. The Kolmogorov-Smirnov test can be done very easily in R Programming Language.

Kolmogorov-Smirnov Test Formula

The formula for the Kolmogorov-Smirnov test can be given as:

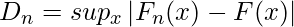
where,

• sup_x : the supremum of the set of distances
• F_n(x) : the empirical distribution function for n id observations X_i

The empirical distribution function is a distribution function that is associated with the empirical measures of the chosen sample. Being a step function, this cumulative distribution jumps up by a 1/n step at each and every n data point. 

One Sample Kolmogorov-Smirnov Test in R

The K-S test can be performed using the ks.test() function in R. 

Syntax:

ks.text(x, y, alternative = c(“two.sided”, “less”, “greater”), exact= NULL, tol= 1e-8, 
simulate.p.value = FALSE, B=2000)

Parameters:

• x: numeric vector of data values
• y: numeric vector of data values or a character string which is used to name a cumulative distribution function.
• alternative: used to indicate the alternate hypothesis.
• exact: usually NULL or it indicates a logic that an exact p-value should be computed.
• tol: an upper bound used for rounding off errors in the data values.
• simulate.p.value: a logic that checks whether to use Monte Carlo method to compute the p-value.
• B: an integer value that indicates the number of replicates to be created while using the Monte Carlo method.

Let us understand how to execute a K-S Test step by step using an example of a two-sample K-S test. First, install the required packages. For performing the K-S test we need to install the “dgof” package using the install.packages() function from the R console.

R

# installing the required package
install.packages("dgof")

After a successful installation of the package, load the required package in our R Script. for that purpose, use the library() function as follows:

R

# loading the required package
library("dgof")

Use the rnorm() function to generate samples say x. The rnorm() function is used to generate random variates.

R

x1 <- rnorm(100)
ks.test(x1, "pnorm")

Output:

    One-sample Kolmogorov-Smirnov test

data:  x1
D = 0.10091, p-value = 0.2603
alternative hypothesis: two-sided

Two Sample Kolmogorov-Smirnov Test in R

Use the rnorm() function and the runif() function to generate samples say x and y. The rnorm() function is used to generate random variates while the runif() function is used to generate random deviates.

R

# generating random variate sample 1
x <- rnorm(50)

# generating random deviates sample 2
y <- runif(30)

Now perform the K-S test on these two samples. For that purpose, use the ks.test() of the dgof package.

R

# performing the K-S Test Do x and y
# come from the same distribution?
ks.test(x, y)

Output:

    Two-sample Kolmogorov-Smirnov test

data:  x and y
D = 0.84, p-value = 5.151e-14
alternative hypothesis: two-sided

Visualization of the Kolmogorov- Smirnov Test in R

Being quite sensitive to the difference in shape and location of the empirical cumulative distribution of the chosen two samples, the two-sample K-S test is efficient, and one of the most general and useful non-parametric tests. Hence we will see how the graph represents the difference between the two samples.

Here we are generating both samples using the rnorm() functions and then plotting them.  

R

# loading the required package
library(dgof)

# sample 1
# generating a random variate
x <- rnorm(50)

# sample 2
# generating a random variate
x2 <- rnorm(50, -1)

# plotting the result
# visualization
plot(ecdf(x),
     xlim = range(c(x, x2)),
     col = "blue")
plot(ecdf(x2),
     add = TRUE,
     lty = "dashed",
     col = "red")

# performing the K-S
# Test on x and x2
ks.test(x, x2, alternative = "l")

Output:

    Two-sample Kolmogorov-Smirnov test

data:  x and x2
D^- = 0.34, p-value = 0.003089
alternative hypothesis: the CDF of x lies below that of y

Visualization of the Kolmogorov- Smirnov Test in R