Why floating-point values do not represent exact value
Last Updated :
28 Mar, 2023
The floating-point numbers serve as rough approximations of mathematical real numbers. They do not represent the exact value. For this reason, we compare the arithmetic results of float variables with a minimum tolerance value.
Example:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
double num1 = 10000.29;
double num2 = 10000.2;
cout << std::setprecision(15)
<< (num1 - num2);
return 0;
}
|
Java
import java.text.DecimalFormat;
class GFG{
public static void main(String[] args)
{
double num1 = 10000.29;
double num2 = 10000.2;
DecimalFormat df = new DecimalFormat(
"#.################");
System.out.println(df.format(num1 - num2));
}
}
|
Python3
if __name__ == '__main__':
num1 = 10000.29;
num2 = 10000.2;
print ("{0:.10f}".format(num1 - num2));
|
C#
using System;
class GFG{
public static void Main(String[] args)
{
double num1 = 10000.29;
double num2 = 10000.2;
Console.WriteLine(
string.Format("{0:F15}",
Decimal.Parse((num1 - num2).ToString())));
}
}
|
Javascript
<script>
let num1 = 10000.29;
let num2 = 10000.2;
document.write(parseFloat(num1-num2));
</script>
|
Output: 0.0900000000001455
The time complexity of this program is O(1) as it only involves simple arithmetic operations and printing the result.
The space complexity is also O(1) as the program only uses a fixed amount of memory to store the two double values and the output.
Explanation:
The expected output is 0.09 as output. But, the output is not 0.09. To understand this, you first have to know how a computer works with float values. When a float variable is initialized, the computer treats it as an exponential value and allocates 4 bytes(32 bits) memory where the mantissa part occupies 24 bits, the exponent part occupies 7 bits, and the remaining 1 bit is used to denote sign.
For type double, the computer does the same but allocates larger memory compared to the float type. In the decimal system, every position from(left to right) in the fractional part is one-tenth of the position to its left. If we move from right to left then every position is 10 times the position to its right.
In a binary system, the factor is two as shown in the table:

To simplify things, let us think of a mythical type named small float(see the above image) which consists of only 5 bits – very small compared to float and double. The first three bits of the type small float will represent mantissa, the last 2 bits will represent the exponent part. For the sake of simplicity, we do not think about the sign. So the mantissa part can have only 8 possible values and the exponent part can only have 4 possible values. See the tables below:
| bit pattern | binary value | decimal value |
|---|
| 000 | (0.000)2 | 0.000 |
| 001 | (0.001)2 | 0.125 |
| 010 | (0.010)2 | 0.250 |
| 011 | (0.011)2 | 0.375 |
| 100 | (0.100)2 | 0.500 |
| 101 | (0.101)2 | 0.625 |
| 110 | (0.110)2 | 0.750 |
| 111 | (0.111)2 | 0.875 |
| Binary pattern | Binary value | Decimal value |
|---|
| 00 | (00)2 | 1 |
| 01 | (01)2 | 2 |
| 10 | (10)2 | 4 |
| 11 | (11)2 | 8 |
So, one combination of mantissa and exponent part can be 11100 where the leftmost two bits represent the exponent part and the remaining three bits represent the mantissa part. The value is calculated as:
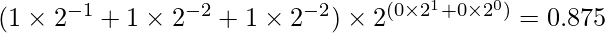
From the two tables, we can easily say that a small float can contain only 32 numbers and the range of the mythical type is 0 to 7. The range is not equally dense. If you see the following image carefully you will see most values lie between 0 and 1. The more you move from right to left the more sparse the numbers will be.

The small float can not represent 1.3, 2.4, 5.6, etc. In that case, small float approximates them. It can not represent numbers bigger than 7. Besides many combinations represent the same value. For example: 00000, 00001, 00010, 00011 represent the same decimal value i.e., (0.000). Twelve of the 32 combinations are redundant.
If we increase the number of bits allocated for small float, the denser portion will increase. As float values reserve 32 bits, float value can represent more numbers compared to small float. But some issues can be observed with float values and double values. There is no path to overcome this. Computers with infinite memory and fast preprocessor can only compute exact float or double values which is a fantasy for us.
Share your thoughts in the comments
Please Login to comment...