Approximate solution for Travelling Salesman Problem using MST
Last Updated :
28 Nov, 2022
We introduced Travelling Salesman Problem and discussed Naive and Dynamic Programming Solutions for the problem in the previous post,. Both of the solutions are infeasible. In fact, there is no polynomial time solution available for this problem as the problem is a known NP-Hard problem. There are approximate algorithms to solve the problem though. The approximate algorithms work only if the problem instance satisfies Triangle-Inequality.
Triangle-Inequality: The least distant path to reach a vertex j from i is always to reach j directly from i, rather than through some other vertex k (or vertices), i.e., dis(i, j) is always less than or equal to dis(i, k) + dist(k, j). The Triangle-Inequality holds in many practical situations.
When the cost function satisfies the triangle inequality, we can design an approximate algorithm for TSP that returns a tour whose cost is never more than twice the cost of an optimal tour. The idea is to use Minimum Spanning Tree (MST). Following is the MST based algorithm.
Algorithm:
- Let 1 be the starting and ending point for salesman.
- Construct MST from with 1 as root using Prim’s Algorithm.
- List vertices visited in preorder walk of the constructed MST and add 1 at the end.
Let us consider the following example. The first diagram is the given graph. The second diagram shows MST constructed with 1 as root. The preorder traversal of MST is 1-2-4-3. Adding 1 at the end gives 1-2-4-3-1 which is the output of this algorithm.
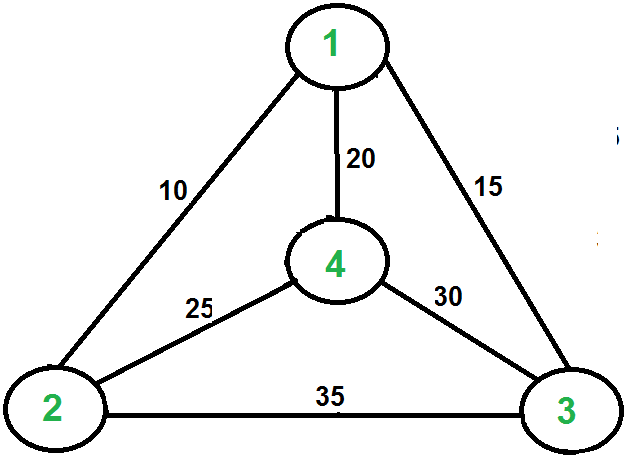
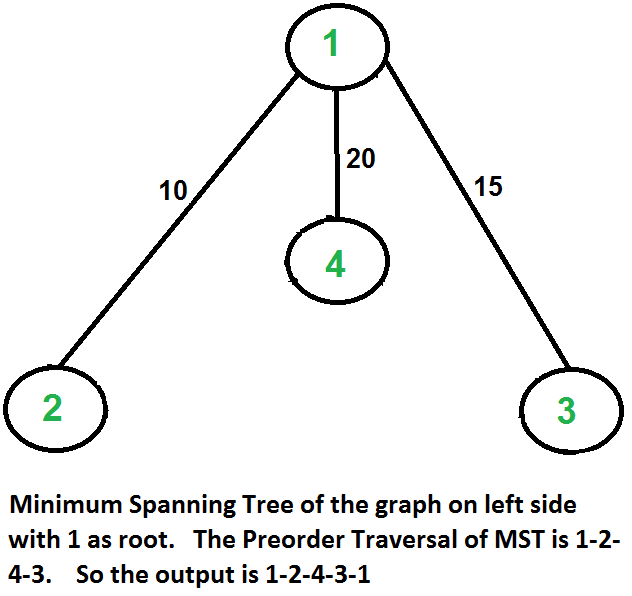
In this case, the approximate algorithm produces the optimal tour, but it may not produce optimal tour in all cases.
How is this algorithm 2-approximate?
The cost of the output produced by the above algorithm is never more than twice the cost of best possible output. Let us see how is this guaranteed by the above algorithm.
Let us define a term full walk to understand this. A full walk is lists all vertices when they are first visited in preorder, it also list vertices when they are returned after a subtree is visited in preorder. The full walk of above tree would be 1-2-1-4-1-3-1.
Following are some important facts that prove the 2-approximateness.
- The cost of best possible Travelling Salesman tour is never less than the cost of MST. (The definition of MST says, it is a minimum cost tree that connects all vertices).
- The total cost of full walk is at most twice the cost of MST (Every edge of MST is visited at-most twice)
- The output of the above algorithm is less than the cost of full walk. In above algorithm, we print preorder walk as output. In preorder walk, two or more edges of full walk are replaced with a single edge. For example, 2-1 and 1-4 are replaced by 1 edge 2-4. So if the graph follows triangle inequality, then this is always true.
From the above three statements, we can conclude that the cost of output produced by the approximate algorithm is never more than twice the cost of best possible solution.
We have discussed a very simple 2-approximate algorithm for the travelling salesman problem. There are other better approximate algorithms for the problem. For example Christofides algorithm is 1.5 approximate algorithm. We will soon be discussing these algorithms as separate posts.
Share your thoughts in the comments
Please Login to comment...