Travelling Salesman Problem | Greedy Approach

Given a 2D matrix tsp[][], where each row has the array of distances from that indexed city to all the other cities and -1 denotes that there doesn’t exist a path between those two indexed cities. The task is to print minimum cost in TSP cycle.
Examples:

Input:
tsp[][] = {{-1, 10, 15, 20}, 
{10, -1, 35, 25}, 
{15, 35, -1, 30}, 
{20, 25, 30, -1}}; 
Below is the given graph: 

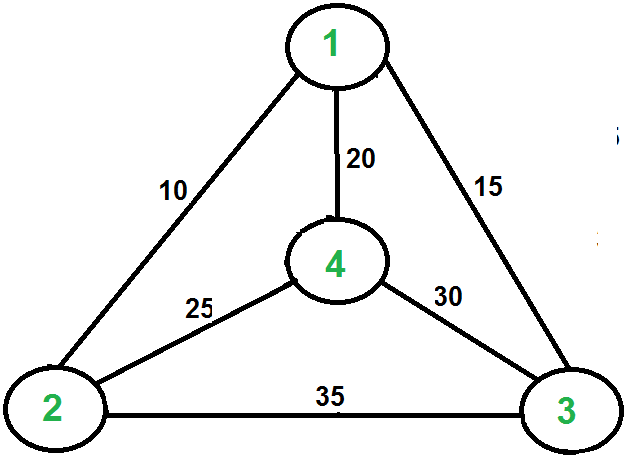
Output: 80 
Explanation:
We are trying to find out the path/route with the minimum cost such that our aim of visiting all cities once and return back to the source city is achieved. The path through which we can achieve that, can be represented as 1 -> 2 -> 4 -> 3 -> 1. Here, we started from city 1 and ended on the same visiting all other cities once on our way. The cost of our path/route is calculated as follows: 
1 -> 2 = 10 
2 -> 4 = 25 
4 -> 3 = 30 
3 -> 1 = 15 
(All the costs are taken from the given 2D Array) 
Hence, total cost = 10 + 25 + 30 + 15 = 80
Input:
tsp[][] = {{-1, 30, 25, 10}, 
{15, -1, 20, 40}, 
{10, 20, -1, 25}, 
{30, 10, 20, -1}}; 
Output: 50 

We introduced Travelling Salesman Problem and discussed Naive and Dynamic Programming Solutions for the problem in the previous post. Both of the solutions are infeasible. In fact, there is no polynomial-time solution available for this problem as the problem is a known NP-Hard problem. There are approximate algorithms to solve the problem though. 
This problem can be related to the Hamiltonian Cycle problem, in a way that here we know a Hamiltonian cycle exists in the graph, but our job is to find the cycle with minimum cost. Also, in a particular TSP graph, there can be many hamiltonian cycles but we need to output only one that satisfies our required aim of the problem.
Approach: This problem can be solved using Greedy Technique. Below are the steps: 

1. Create two primary data holders: 
   • A list that holds the indices of the cities in terms of the input matrix of distances between cities.
   • Result array which will have all cities that can be displayed out to the console in any manner.
2. Perform traversal on the given adjacency matrix tsp[][] for all the city and if the cost of the reaching any city from current city is less than current cost the update the cost.
3. Generate the minimum path cycle using the above step and return there minimum cost.

Below is the implementation of the above approach:

C++

//  C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the minimum
// cost path for all the paths
void findMinRoute(vector<vector<int> > tsp)
{
    int sum = 0;
    int counter = 0;
    int j = 0, i = 0;
    int min = INT_MAX;
    map<int, int> visitedRouteList;

    // Starting from the 0th indexed
    // city i.e., the first city
    visitedRouteList[0] = 1;
    int route[tsp.size()];

    // Traverse the adjacency
    // matrix tsp[][]
    while (i < tsp.size() && j < tsp[i].size())
    {

        // Corner of the Matrix
        if (counter >= tsp[i].size() - 1)
        {
            break;
        }

        // If this path is unvisited then
        // and if the cost is less then
        // update the cost
        if (j != i && (visitedRouteList[j] == 0))
        {
            if (tsp[i][j] < min)
            {
                min = tsp[i][j];
                route[counter] = j + 1;
            }
        }
        j++;

        // Check all paths from the
        // ith indexed city
        if (j == tsp[i].size())
        {
            sum += min;
            min = INT_MAX;
            visitedRouteList[route[counter] - 1] = 1;
            j = 0;
            i = route[counter] - 1;
            counter++;
        }
    }

    // Update the ending city in array
    // from city which was last visited
    i = route[counter - 1] - 1;

    for (j = 0; j < tsp.size(); j++)
    {

        if ((i != j) && tsp[i][j] < min)
        {
            min = tsp[i][j];
            route[counter] = j + 1;
        }
    }
    sum += min;

    // Started from the node where
    // we finished as well.
    cout << ("Minimum Cost is : ");
    cout << (sum);
}

// Driver Code
int main()
{

    // Input Matrix
    vector<vector<int> > tsp = { { -1, 10, 15, 20 },
                                 { 10, -1, 35, 25 },
                                 { 15, 35, -1, 30 },
                                 { 20, 25, 30, -1 } };

    // Function Call
    findMinRoute(tsp);
}

// This code is contributed by grand_master.

Java

// Java program for the above approach
import java.util.*;

public class TSPGreedy {

    // Function to find the minimum
    // cost path for all the paths
    static void findMinRoute(int[][] tsp)
    {
        int sum = 0;
        int counter = 0;
        int j = 0, i = 0;
        int min = Integer.MAX_VALUE;
        List<Integer> visitedRouteList
            = new ArrayList<>();

        // Starting from the 0th indexed
        // city i.e., the first city
        visitedRouteList.add(0);
        int[] route = new int[tsp.length];

        // Traverse the adjacency
        // matrix tsp[][]
        while (i < tsp.length
               && j < tsp[i].length) {

            // Corner of the Matrix
            if (counter >= tsp[i].length - 1) {
                break;
            }

            // If this path is unvisited then
            // and if the cost is less then
            // update the cost
            if (j != i
                && !(visitedRouteList.contains(j))) {
                if (tsp[i][j] < min) {
                    min = tsp[i][j];
                    route[counter] = j + 1;
                }
            }
            j++;

            // Check all paths from the
            // ith indexed city
            if (j == tsp[i].length) {
                sum += min;
                min = Integer.MAX_VALUE;
                visitedRouteList.add(route[counter] - 1);
                j = 0;
                i = route[counter] - 1;
                counter++;
            }
        }

        // Update the ending city in array
        // from city which was last visited
        i = route[counter - 1] - 1;

        for (j = 0; j < tsp.length; j++) {

            if ((i != j) && tsp[i][j] < min) {
                min = tsp[i][j];
                route[counter] = j + 1;
            }
        }
        sum += min;

        // Started from the node where
        // we finished as well.
        System.out.print("Minimum Cost is : ");
        System.out.println(sum);
    }

    // Driver Code
    public static void
        main(String[] args)
    {
        // Input Matrix
        int[][] tsp = {
            { -1, 10, 15, 20 },
            { 10, -1, 35, 25 },
            { 15, 35, -1, 30 },
            { 20, 25, 30, -1 }
        };

        // Function Call
        findMinRoute(tsp);
    }
}

C#

// C# program for the above approach
using System;
using System.Collections.Generic;

class TSPGreedy{

// Function to find the minimum
// cost path for all the paths
static void findMinRoute(int[,] tsp)
{
    int sum = 0;
    int counter = 0;
    int j = 0, i = 0;
    int min = int.MaxValue;

    List<int> visitedRouteList = new List<int>();

    // Starting from the 0th indexed
    // city i.e., the first city
    visitedRouteList.Add(0);
    int[] route = new int[tsp.Length];

    // Traverse the adjacency
    // matrix tsp[,]
    while (i < tsp.GetLength(0) &&
           j < tsp.GetLength(1))
    {

        // Corner of the Matrix
        if (counter >= tsp.GetLength(0) - 1)
        {
            break;
        }

        // If this path is unvisited then
        // and if the cost is less then
        // update the cost
        if (j != i &&
            !(visitedRouteList.Contains(j)))
        {
            if (tsp[i, j] < min)
            {
                min = tsp[i, j];
                route[counter] = j + 1;
            }
        }
        j++;

        // Check all paths from the
        // ith indexed city
        if (j == tsp.GetLength(0))
        {
            sum += min;
            min = int.MaxValue;
            visitedRouteList.Add(route[counter] - 1);

            j = 0;
            i = route[counter] - 1;
            counter++;
        }
    }

    // Update the ending city in array
    // from city which was last visited
    i = route[counter - 1] - 1;

    for(j = 0; j < tsp.GetLength(0); j++)
    {
        if ((i != j) && tsp[i, j] < min)
        {
            min = tsp[i, j];
            route[counter] = j + 1;
        }
    }
    sum += min;

    // Started from the node where
    // we finished as well.
    Console.Write("Minimum Cost is : ");
    Console.WriteLine(sum);
}

// Driver Code
public static void Main(String[] args)
{

    // Input Matrix
    int[,] tsp = { { -1, 10, 15, 20 },
                   { 10, -1, 35, 25 },
                   { 15, 35, -1, 30 },
                   { 20, 25, 30, -1 } };

    // Function call
    findMinRoute(tsp);
}
}

// This code is contributed by Amit Katiyar

Python3

#  Python3 program for the above approach

from typing import DefaultDict


INT_MAX = 2147483647

# Function to find the minimum
# cost path for all the paths
def findMinRoute(tsp):
    sum = 0
    counter = 0
    j = 0
    i = 0
    min = INT_MAX
    visitedRouteList = DefaultDict(int)

    # Starting from the 0th indexed
    # city i.e., the first city
    visitedRouteList[0] = 1
    route = [0] * len(tsp)

    # Traverse the adjacency
    # matrix tsp[][]
    while i < len(tsp) and j < len(tsp[i]):

        # Corner of the Matrix
        if counter >= len(tsp[i]) - 1:
            break

        # If this path is unvisited then
        # and if the cost is less then
        # update the cost
        if j != i and (visitedRouteList[j] == 0):
            if tsp[i][j] < min:
                min = tsp[i][j]
                route[counter] = j + 1

        j += 1

        # Check all paths from the
        # ith indexed city
        if j == len(tsp[i]):
            sum += min
            min = INT_MAX
            visitedRouteList[route[counter] - 1] = 1
            j = 0
            i = route[counter] - 1
            counter += 1

    # Update the ending city in array
    # from city which was last visited
    i = route[counter - 1] - 1

    for j in range(len(tsp)):

        if (i != j) and tsp[i][j] < min:
            min = tsp[i][j]
            route[counter] = j + 1

    sum += min

    # Started from the node where
    # we finished as well.
    print("Minimum Cost is :", sum)


# Driver Code
if __name__ == "__main__":

    # Input Matrix
    tsp = [[-1, 10, 15, 20], [10, -1, 35, 25], [15, 35, -1, 30], [20, 25, 30, -1]]

    # Function Call
    findMinRoute(tsp)

Javascript

// Javascript program for the above approach

// Function to find the minimum
// cost path for all the paths
function findMinRoute(tsp)
{
    let sum = 0;
    let counter = 0;
    let j = 0, i = 0;
    let min = Number.MAX_SAFE_INTEGER;
    let visitedRouteList=Array(tsp.length).fill(0);

    // Starting from the 0th indexed
    // city i.e., the first city
    visitedRouteList[0] = 1;
    let route = Array(tsp.length);

    // Traverse the adjacency
    // matrix tsp[][]
    while (i < tsp.length && j < tsp[i].length)
    {

        // Corner of the Matrix
        if (counter >= tsp[i].length - 1)
        {
            break;
        }

        // If this path is unvisited then
        // and if the cost is less then
        // update the cost
        if (j != i && (visitedRouteList[j] == 0))
        {
            if (tsp[i][j] < min)
            {
                min = tsp[i][j];
                route[counter] = j + 1;
            }
        }
        j++;

        // Check all paths from the
        // ith indexed city
        if (j == tsp[i].length)
        {
            sum += min;
            min = Number.MAX_SAFE_INTEGER;
            visitedRouteList[route[counter] - 1] = 1;
            j = 0;
            i = route[counter] - 1;
            counter++;
        }
    }

    // Update the ending city in array
    // from city which was last visited
    i = route[counter - 1] - 1;

    for (j = 0; j < tsp.length; j++)
    {

        if ((i != j) && tsp[i][j] < min)
        {
            min = tsp[i][j];
            route[counter] = j + 1;
        }
    }
    sum += min;

    // Started from the node where
    // we finished as well.
    console.log("Minimum Cost is : ");
    console.log(sum);
}

// Driver Code

    // Input Matrix
    let tsp = [ [ -1, 10, 15, 20 ], [ 10, -1, 35, 25 ],
                [ 15, 35, -1, 30 ], [ 20, 25, 30, -1 ] ];

    // Function Call
    findMinRoute(tsp);

// This code is contributed by Pushpesh Raj.

Output

Minimum Cost is : 80

Time Complexity: O(N²*log₂N) 
Auxiliary Space: O(N)