TCS Placement Paper | MCQ 4
Last Updated :
11 Jan, 2023
This is a TCS model placement paper for aptitude preparation. This placement paper will cover aptitude questions that are asked in TCS recruitment drives and also strictly follows the pattern of questions asked in TCS interviews. It is recommended to solve each one of the following questions to increase your chances of clearing the TCS interview.

- A call centre agent has a list of 305 phone numbers of people in alphabetical order of names, but Anuj does not have any of the names. He needs to quickly contact Danish Mank to convey a message to him. If each call takes 2 minutes to complete, and every call is answered, what is the minimum amount of time during which he can guarantee to deliver the message to Danish?
a) 206 minutes
b) 610 minutes
c) 18 minutes
d) 34 minutes
Answer: c) 18 minutes
Solution:
We need to search for a particular name in a phone book. So we need to apply a method in which we can easily search a number in a minimum count. So we divide the list into two equal halves, i.e., 305/2 = 152.5 or let’s take 152. Now we can decide whether to check for Danish in the upper or lower half of 152. This is decided by the starting letter of the name in a page. Proceeding in the similar manner we get,
152/2 = 76
76/2 = 38
38/2 = 19
19/2 = 9
9/2 = 4
4/2 = 2
2/2 = 0
So we get 0 at the 9th time, hence this is the minimum number of the count to find Danish. So total time taken = 9 * 2 = 18 minutes.
2. There is an office consisting of 38 people. 10 of them like to play golf, 15 like to play football and 20 neither play golf nor football. How many like both golf and football?
a) 10
b) 7
c) 15
d) 18
Answer: b) 7
Solution:
Let the number of people liking golf = ‘A’
Let the number of people liking football = ‘B’
Let the number of people liking either golf or football = A U B = 38 – 20 = 18
People liking both golf and football =
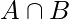
= A + B – AUB = 10 + 15 -18 = 7
3. If a dice is rolled 2 times, what is the probability of getting a pair of numbers with sum equal to 3 or 4?
a) 6/36
b) 5/36
c) 1/9
d) 1/12
Answer: b) 5/36
Solution:
Total probability = 36
We can get a sum of 3 or 4 in this many ways:
=> (2, 1), (1, 2), (1, 3), (3, 1), (2, 2) = 5
So probability = 5 / 36
4. A shopkeeper charges 12 rupees for a bunch of cakes. Anuj bargained to the shopkeeper and got two extra ones, and that made them cost one rupee for dozen less than first asking price. How many cakes did Anuj receive in 12 rupees?
a) 10
b) 14
c) 18
d) 16
Answer: d) 16
Solution:
Let the number of cakes = ‘x’ or ‘x/12’ dozen
So, x/12 cost Anuj 12 rupees, or 1 dozen cost him = 144/x rupees
Now, he gets two extra = 144/(x+2) in 1 rupees less,
=> 144/x – 144/(x+2) = 1
=> On putting 16, the equation is satisfied, hence the answer.
5. Ram alone can do 1/4th of the work in 2 days. Shyam alone can do 2/3th of the work in 4 days. So what part of the work must be done by Anil in 2 days, for them to complete the work together in 3 days?
a) 1/8
b) 1/20
c) 1/16
d) 1/12
Answer: d) 1/12
Solution:
Ram alone can complete the work in 2*4 = 8 days.
Shyam alone can complete the work in 4*(3/2) = 6 days.
Taking the lcm of 8, 6, 3 = 24
Capacity of Ram = 24/8 = 3
Capacity of Shyam = 24/6 = 4
Capacity of Anil = 8 – (4+3) = 1
Now in 2 days Anil can do 2 unit of work = 2/24 = 1/12 part of the work
OR
Let C’s one day work be x.
Acc. to question
1/8 + 1/6 + x = 1/3
x = 1/24
Therefore C will complete 1/12th of the work in 2 days.
6. Mr Mehta chooses a number and keeps on doubling the number followed by subtracting one from it. If he chooses 3 as the initial number and he repeats the operation 30 times then what is the final result?
a) (2^30) – 1
b) (2^30) – 2
c) (2^31) – 1
d) None of these
Answer: d) None of these
Solution:
According to the question,
3 * 2 – 1 = 5 =
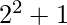
5 * 2 – 1 = 9 =
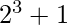
9 * 2 – 1 = 17 =
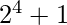
Proceeding in the similar fashion, on 30 times we get
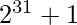
7. Ram alone can paint a wall in 7 days and his friend Roy alone paints the same wall in 9 days. In how many days they can paint the wall working together? (Round off your answer)
a) 3
b) 5
c) 4
d) 7
Answer: c) 4
Solution:
This can be solved by applying a simple formula = ab/(a+b)
or, (9*7)/(9+7)
or, 63/16 = 3.9375 = 4 (answer)
8. Two vertical walls of the length of 6 meters and 11 meters are at a distance of 12 meters apart. Find the top distance of both walls?
a) 15 meters
b) 13 meters
c) 12 meters
d) 10 meters
Answer: b) 13 meters
Solution:
Let’s consider this figure,

We need to find the distance of AB,
We know AC = 12 m and BC = 11-6 = 5 m
So applying pythagoras theorem we get,
AB =
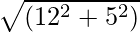
= 13 meters
9. For f(m, n) =45*m + 36*n, where m and n are integers (either positive or negative). What is the minimum positive value for f(m, n) for all values of m, n (this may be achieved for various values of m and n)?
a) 18
b) 12
c) 9
d) 16
Answer: c) 9
Solution:
To get the minimum value of f(m, n), put m = 1 and n = -1, we get
f(, n) = 9
10. A white cube(with six faces) is to be painted blue on two different faces. In how many different ways can this be achieved (two paintings are considered same if on a suitable rotation of the cube one painting can be carried to the other)?
a) 30 ways
b) 18 ways
c) 4 ways
d) 2 ways
Answer: d) 2
Solution:
This can be achieved in the following different ways;:
First, painting on opposite faces can be achieved in 1 way.
Second, painting on adjacent faces can be achieved in 1 way.
Therefore in 2 ways.
Share your thoughts in the comments
Please Login to comment...