TCS Placement Paper | MCQ 5
Last Updated :
11 Jan, 2023
This is a TCS model placement paper for aptitude preparation. This placement paper will cover aptitude questions that are asked in TCS recruitment drives and also strictly follows the pattern of questions asked in TCS interviews. It is recommended to solve each one of the following questions to increase your chances of clearing the TCS interview.

- Which of the following numbers must be added to 5678 to give a remainder 35 when divided by 460?
a) 980
b) 618
c) 955
d) 797
Answer: d) 797
Solution:
Let the number added to 5678 be x to give a remainder 35 and quotient k when divided by 460.
So, 5678 + x = 460k + 35
or, 5643 + x = 460k
So 5643 + x must be divisible by 460
Analyzing from the options, we get on adding 797 to 5643, the number 6440 is divisible by 460.
- Rahaman went to a stationery shop and bought 18 pencils for Rs.100. He paid 1 rupee more for each grey pencil than for each black pencil. What is the price of a grey pencil and how many grey pencils did he buy?
a) Rs.5, 10
b) Rs.6, 10
c) Rs.5, 8
d) Rs.6, 8
Answer: b) Rs. 6, 10
Solution:
The best way is to analyse from the mentions.
Let’s take option b in which 10 pencils are bought at Rs.6 each. So total cost of grey pencils = 6 * 10 = Rs.60. So Rahaman is left with 40 rupees. He buys 8 black pencils at Rs 5 each which is 1 rupee less than what he had spent in buying the grey ones. Thus satisfying the conditions.
- Four people each roll a four die once. Find the probability that at least two people will roll the same number?
a. 13/18
b. 5/18
c. None of the above
d. 1295/1296
Answer: a) 13/18 ways
Solution:
Total possible outcomes = 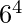 = 1296
= 1296
Number of ways in which no two people get same number = 6*5*4*3 = 360 ways
The probability of no two people getting the same number = 360 / 1296 ways = 5/18 ways
So the probability of at least two people getting the same number = 1 – 5/18 = 13/18 ways
- Ram said Shyam “If you give me half your money I will have Rs.75.” Shyam said, “If you give me one-third of your money, I will have Rs.75 How much money did Shyam have4
c) 48
d) 60
Answer: d) 60
Solution: Let Ram and Shyam be denoted by ‘R’ and ‘S’ respectively
According to the question,
Eqn 1. R + S/2 = 75
Eqn 2. R/3 + S = 75
Therefore, solving both the equations we get, R = 45 and S = 60.
- Ram goes to the market to buy apples. If he can bargain and reduce the price per apple by Rs.2, he can buy 30 apples instead of 20 apples with the money he has. How much money does he have?
a. Rs.100
b. Rs.50
c. Rs.120
d. Rs.150
Answer: c) 120
Solution: Let the price per orange be Rs. x.
So total money Ram has in buying at original price = 20x.
On reducing the price by 2 rupees each the total money must be (x-2)*30
According to the question,
20x = (x-2)*30
On solving this we get x = 6 or the total money = Rs. 120
- How many positive integers less than 500 can be formed using the numbers 1, 2, 3, and 5 for digits, each digit being used only once.
a) 68
b) 34
c) 66
d) 52
Answer: b) 34
Solution:
Single digit numbers can be formed in 4 ways.
2 digit number can be formed in 4 * 3 = 12 ways
3 digit number less than 500 can be formed in 3 * 3 * 2 = 18 ways.
Total number of ways = 18 + 12 + 4 = 34 ways
- A boy entered a shop and bought x number of books for y rupees. When he was about to leave the bookkeeper said, “if you buy 10 more books, you can have all the books for 2 rupees and you will also save 80 cents a dozen”. So what are x and y?
a) (5, 1)
b) (10, 1)
c) (15, 1)
d) Cannot be determined.
Answer: a) (5, 1)
Solution:
x number of books cost him y rupees.
So, 1 book will cost him y/x rupees.
12 books will cost him rupees 12 y/x.
The shopkeeper says,
x + 10 books cost him 12 rupees
1 book will cost him 12/(x+10) rupees
12 books will cost him 24/(x+10) rupees
We know that 80 cents = 4/5 of a dollar,
So, 12y/x – 24/(10+x) = 4/5
Analysing the given choices, we get (5, 1) satisfies the equation.
- The perimeter of an equilateral triangle is equal to a regular hexagon. Find out the ratio of their areas?
a. 3:2
b. 1:6
c. 2:3
d. 6:1
Answer: c) 2:3
Solution:Let the side of the equilateral triangle be a unit and that of the regular hexagon be b unit.
So perimeter of the triangle = 3a and perimeter of the hexagon is 6b unit.
or, 3a = 6b
or a/b = 2/1
The area of the equilateral tr
iangle = 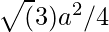
The area of the regular hexagon = 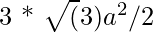
or, 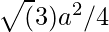 :
: 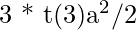
Solving this and substituting a/b we get the answer as 2 : 3
- In the given series: 70, 54, 45, 41……. What will be the next number?
a) 40
b) 36
c) 35
d) 38
Answer: a) 40
Solution:The series goes like:
70 – 54 = 16 (4^2)
54 – 45 = 9 (3^2)
45 – 41 = 4 (2^2)
41 – 40 = 1 (1^1)
- A series of story books were published at an interval of seven years. When the seventh book was published the total sum of the publication year was 13524. In which year was the first book published?
a) 1910
b) 1911
c) 2002
d) 1932
Answer: b) 1911
Solution:We get the series of publications as n, n+7, n+14, n+21, n+28, n+35, n+42.
Sum of publications = 13524 = 7/2[2n + (7-1)*7] (Using the sum of AP formula)
We get, n = 1911 (answer)
Share your thoughts in the comments
Please Login to comment...