TCS Placement Paper | MCQ 1
Last Updated :
11 Jan, 2023
This is a TCS model placement paper for aptitude preparation. This placement paper will cover aptitude questions that are asked in TCS recruitment drives and also strictly follows the pattern of questions asked in TCS interviews. It is recommended to solve each one of the following questions to increase your chances of clearing TCS interview. 
- An exam was conducted and the following was analyzed. 4 men were able to check some exam papers in 8 days working 5 hours regularly. What is the total number of hours taken by 2 men in 20 days to check double the number of exam papers?
Answer: 8 hours
- Solution:
Assuming that 1 unit of work is done in 1 hour Let’s calculate the total number of working hours: => 4 * 8 * 5 = 160 units Now the work is doubled: => 160 * 2 = 320 units Let ‘x’ be the number of hours taken by 2 men to complete the work in 20 days. Therefore, => 2 * 20 * x = 320 => x = 8 hours (Answer).
- The numbers from 101 to 150 are written as, 101102103104105…146147148149150. What will be the remainder when this total number is divided by 3?
Answer: 2
- Solution:
The divisibility rule for 3 is that the sum of all digits of a number should be divisible by 3. Let’s calculate the sum of the digits: There are 50 1’s (unit place) = 50 There are 10 1’s (tens place) = 10 There are 10 2’s (tens place) = 20 There are 10 3’s (tens place) = 30 There are 10 4’s (tens place) = 40 There is one 5 (tens place) = 5 For each number 1 to 9, there are 5 sets of sum 45(1+2+…+9) = 225 => So sum of all digits = 380 => 380 / 3 = 2 (Answer)
- If the alphabets are written in the sequence of a, bb, ccc, dddd, eeeee, ffffff, …. What will be the 120th letter?
Answer: O
- Solution:
It can be seen that the letter are in AP sequence, So applying the formula we get, 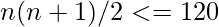 We find that n = 15 fits the equation The 15th letter in the English alphabet = O So 15th term contains O.
We find that n = 15 fits the equation The 15th letter in the English alphabet = O So 15th term contains O.
- There is a tank whose 1/7 th part is filled with fuel. If 22 liters of fuel is poured into the tank, the indicator rises to 1/5 th mark of the tank. So what is the total capacity of the tank?
Answer: 385
- Solution:
Let the total capacity of the tank be ‘x’ liters. According to the question, => x/7 + 22 = x/5 => x/5 – x/7 = 22 => x = 385 litres(Answer)
- How many prime numbers lie between 3 and 100 (excluding the values) that satisfies the condition:
- In the given figure, find the ratio of area of the square to area of the triangle:
 a) 3:2 b) 2:3 c) 2:1 d) 1:2
a) 3:2 b) 2:3 c) 2:1 d) 1:2
Answer: c) 2:1
- Solution:
Let the side of the square be ‘2’ units Area of the square = (side)^2 = 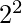 = 4 unit Side of triangle, using Pythagoras Theorem =
= 4 unit Side of triangle, using Pythagoras Theorem = 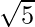 unit Height of triangle = side of square (Using Pythagorean theorem) Area of triangle = 1/2 * base * height here, base = height = side Area of triangle = 1/2 * (side)^2 => 1/2 *2 * 2 => 2 units Therefore the ratio = 4:2 => 2:1 (Answer)
unit Height of triangle = side of square (Using Pythagorean theorem) Area of triangle = 1/2 * base * height here, base = height = side Area of triangle = 1/2 * (side)^2 => 1/2 *2 * 2 => 2 units Therefore the ratio = 4:2 => 2:1 (Answer)
- There is a fairy island where lives a Knight, a Knave, and a Spy. You go there and meet three people suppose A, B, and C, one of whom is a knight, one a knave, and one a spy. It is known that the knight always tells the truth, the knave always lies, and the spy can either lie or tell the truth.
- Find the number of perfect squares in the given series 2013, 2020, 2027, ……………., 2300? (Hint 44^2=1936) a) 2 b) 1 c) 3 d) None of the above
Answer: b) 1
- Solution:
We can see that the series is in the form of AP with common difference of 7. So the series is in the form of 2013 + 7d The hint is actually a shortcut: 44^2 = 1936 45^2 = 2025 46^2 = 2116 47^2 = 2209 48^2 = 2304 Therefore among these numbers, we need to find which of them are in the form of 2013 + 7d Only one number 2209 can be written in the form 2013 + 7*28. Therefore the answer is 1.
- In the series of 7^1+7^2+7^3+7^4…….+7^204+7^205, how many numbers are there with the unit place as 3?
Answer: 51
Solution: According to the cyclicity of 7, the unit digit follows the pattern of 7, 9, 3, 1 and this repeats. So in every 4 numbers, we get one 3 in the unit place. Dividing 205 by 4 we get 51 which is the answer to the following question.
- Find the number of divisors of 1728(including 1 and the number itself).
Answer: 28
- Solution:
There is a direct formula for this: Number =  where p, q and r are prime numbers. Simply we need to prime factorize the Number. Then, (a+1).(b+1).(c+1) is the number of divisors. For 1728 =
where p, q and r are prime numbers. Simply we need to prime factorize the Number. Then, (a+1).(b+1).(c+1) is the number of divisors. For 1728 = 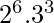 Therefore, (6+1).(3+1) = 28
Therefore, (6+1).(3+1) = 28
Share your thoughts in the comments
Please Login to comment...