Static Hazards in Digital Logic
Last Updated :
24 Mar, 2023
A hazard, if exists, in a digital circuit causes a temporary fluctuation in the output of the circuit. In other words, a hazard in a digital circuit is a temporary disturbance in the ideal operation of the circuit which if given some time, gets resolved itself. These disturbances or fluctuations occur when different paths from the input to output have different delays and due to this fact, changes in input variables do not change the output instantly but do appear at the output after a small delay caused by the circuit-building elements, i.e., logic gates. There are three different kinds of hazards found in digital circuits
IN OTHER WORDS,
Consider a logic circuit that is expected to give a logic -1 output momentarily becomes logic-0, because of finite propagation delays of various gates this unwanted switching transient is called HAZARDS.
- Static hazard
- Dynamic hazard
- Functional hazard
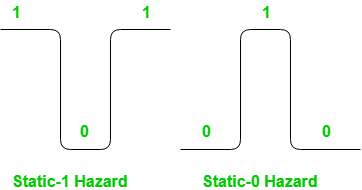
We will discuss only static hazards here to understand them completely. Formally, a static hazard takes place when the change in input causes the output to change momentarily before stabilizing to its correct value. Based on what is the correct value, there are two types of static hazards, as shown below in the image:
- Static-1 Hazard: Static-1 Hazards occur in SOP (SUM-OF-PRODUCT) circuit.
- If the output is currently at logic state 1 and after the input changes its state, the output momentarily changes to 0 before settling on 1, then it is a Static-1 hazard.
- In response to an input change & for some combination of PROPAGATION DELAY a logic circuit may go to zero (0) when it should remain constant at one (1) this transient is called a STATIC-1 Hazards as shown in the figure below.
- Static-0 Hazard: Static-0 Hazards occur in the POS (PRODUCT-OF-SUM) circuit.
- If the output is currently at logic state 0 and after the input changes its state, the output momentarily changes to 1 before settling on 0, then it is a Static-0 hazard.
- In response to an input change & for some combination of PROPAGATION DELAY a logic circuit may go to one (1) when it should remain constant at zero (0) this transient is called a STATIC-1 Hazards as shown in the figure below.
Detection of Static hazards using K-map:
Let us consider static-1 hazard first.
To detect a static-1 hazard for a digital circuit following steps are used:
- Step-1: Write down the output of the digital circuit, say Y.
- Step-2: Draw the K-map for this function Y and note all adjacents 1’s.
- Step-3: If there exists any pair of cells with 1’s which do not occur to be in the same group ( i.e. prime implicant), it indicates the presence of a static-1 hazard. Each such pair is a static-1 hazard.
Let’s have an example: Example – Consider the circuit shown below. 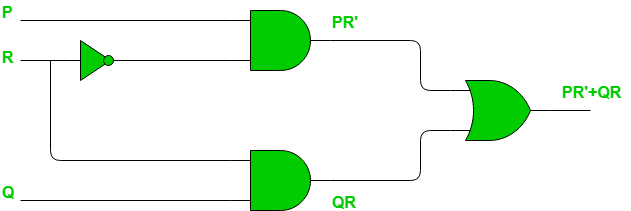
We have output, say F, as: 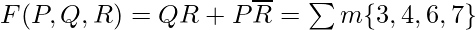 Lets draw the K-map for this
Lets draw the K-map for this
Boolean function as follows: 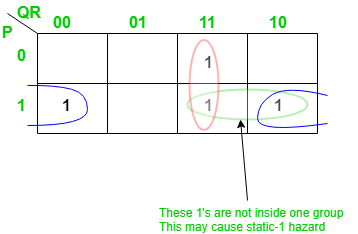
The pair of 1’s encircled as green is not part of the grouping/pairing provided by the output of this Boolean function. This will cause a static-1 hazard in this circuit. Removal of static-1 hazard: Once detected, a static-1 hazard can be easily removed by introducing some more terms (logic gates) to the function (circuit). The most common idea is to add the missing group in the existing Boolean function, as adding this term would not affect the function by any means but it will remove the hazard. Since in the above example the pair of 1’s encircled with blue color causes the static-1 hazard, we just add this as a prime implicant to the existing function as follows: 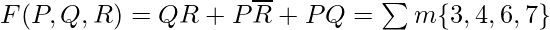 Note that there is no difference in the number of minterms of this function. The reason is that the static-1 hazards are based on how we group 1’s (or 0’s for static-0 hazard) for a given set of 1’s in the K-map. Thus it does not make any difference in the number of 1’s in the K-map. The circuit would look as shown below with the change made for the removal of the static-1 hazard.
Note that there is no difference in the number of minterms of this function. The reason is that the static-1 hazards are based on how we group 1’s (or 0’s for static-0 hazard) for a given set of 1’s in the K-map. Thus it does not make any difference in the number of 1’s in the K-map. The circuit would look as shown below with the change made for the removal of the static-1 hazard. 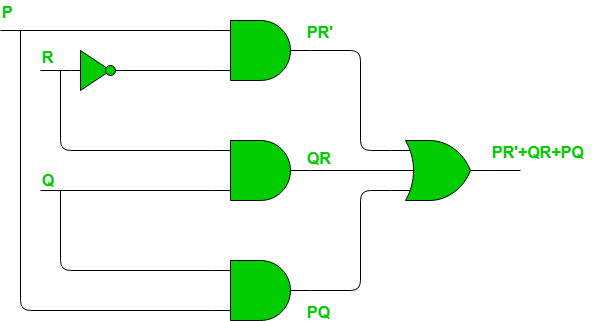
Similarly, for Static-0 Hazards, we need to consider 0’s instead of 1’s, and if any adjacent 0’s in K-map are not grouped into the same group that may cause a static-0 hazard. The method to detect and resolve the static-0 hazard is completely the same as the one we followed for the static-1 hazard except that instead of SOP, POS will be used as we are dealing with 0’s in this case.
Share your thoughts in the comments
Please Login to comment...