Sorting by combining Insertion Sort and Merge Sort algorithms
Last Updated :
14 Feb, 2022
Insertion sort: The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
Advantages: Following are the advantages of insertion sort:
- If the size of the list to be sorted is small, insertion sort runs faster
- Insertion sort takes O(N) time when elements are already sort
- It is an in-place algorithm O(1), no auxiliary space is required
Merge sort: Merge Sort is a Divide and Conquer algorithm. It divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves.
Advantages: Following are the advantages of merge sort:
- The division of the main problem into sub-problem has no major cost
From the above two comparisons, the advantages of both the sorting algorithms can be combined, and the resulting algorithm will have time complexity O(N[K+log(N/K)]). Below is the derivation of the time complexity of this combined algorithm:
Let, no. of elements in the list = N
Divide:
- We first divide these N elements into (N/K) groups of size K
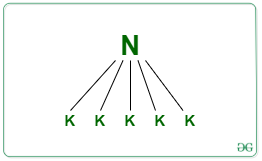
Sorting:
- For each division of subarray of size K, perform the insertion sort operation to sort this subarray
- The total cost of insertion sort for a single block of K elements:
- For best case: O(K)
- For worst case: O(
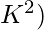
- Since there are (N/K) such blocks each of size K, we get the total cost of applying insertion sort as:
- For best case: (N/K) * K = O(N) <– (1)
- For worst case: (N/K) * K^{2} = O(NK) <– (2)
Merging:
- After applying Insertion sort on (N/K) groups each of K sorted elements
- For merging these (N/K) groups:
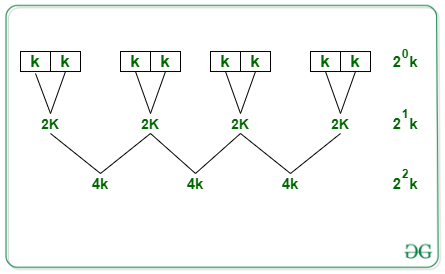
- Let’s say we take i iterations of merge sort. So, for the loop to stop we will need to equate as:
- (2^i) * K = N
- (2^i) = N/K
- i*log(2) = log(N/K) Taking log on both sides
- i = log(N/K)
- Cost of merging = O(N)
- Total cost of merging = No. of iteration * Cost of iteration
- = log(N/K)*N
- = N*log(N/K)
- = O(N*Log(N/K)) <– (3)
The total cost of the algorithm (insertion + merge) is:
- Best case: N+Nlog(N/K) <– from (1) and (3)
- Worst case: NK + Nlog(N/K) <– from (2) and (3)
If K = 1, then it is complete merge sort which is better in terms of time complexity
If K = N, then it is complete Insertion sort which is better in terms of space complexity
Share your thoughts in the comments
Please Login to comment...