Role of Log Odds in Logistic Regression
Last Updated :
22 Oct, 2021
Prerequisite : Log Odds, Logistic Regression
NOTE: It is advised to go through the prerequisite topics to have a clear understanding of this article.
Log odds play an important role in logistic regression as it converts the LR model from probability based to a likelihood based model. Both probability and log odds have their own set of properties, however log odds makes interpreting the output easier. Thus, using log odds is slightly more advantageous over probability.
Before getting into the details of logistic regression, let us briefly understand what odds are.
Odds : Simply put, odds are the chances of success divided by the chances of failure. It is represented in the form of a ratio. (As shown in equation given below)
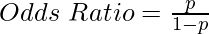
where,
p -> success odds
1-p -> failure odds
Logistic Regression with Log odds
Now, let us get into the math behind involvement of log odds in logistic regression. In logistic regression, the odds of independent variable corresponding to a success is given by:
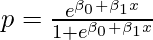
where,
p -> odds of success
β0, β1 -> assigned weights
x -> independent variable
So, the odds of failure in this case will be given by:
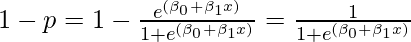
Therefore, the odds ratio is defined as:
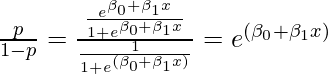
Now, as discussed in the log odds article, we take the log of the odds ratio to get symmetricity in the results. Therefore, taking log on both sides gives:
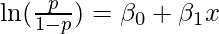
which is the general equation of logistic regression. Now, in the logistic model, L.H.S contains the log of odds ratio that is given by the R.H.S involving a linear combination of weights and independent variables.
Graphical Intuition
i. Problem with Probability based output in Logistic Regression
Let us consider an example. Say, we build a logistic regression model to determine the probability of a person suffering from diabetes based on their sugar level. The plot for this would look like: (See Fig 1)
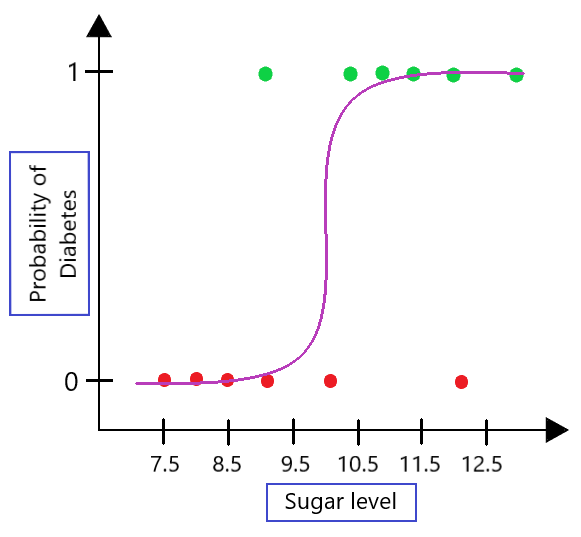
Fig 1 : LR model plot
The problem remains that the output of the model is only binary based on the above plot. To tackle this problem, we use the concept of log odds present in logistic regression.
ii. Solution: Transforming Output
To solve the above discussed problem, we convert the probability-based output to log odds based output. (As shown in equation given below)
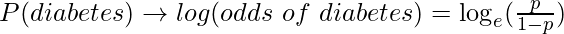
Let us assume random values of p and see how the y-axis is transformed.
a. Boundary values
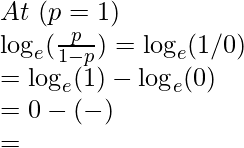
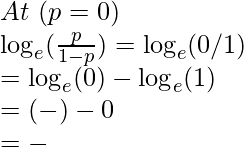
So, the domain of y axis is: (-∞, ∞)
b. Middle value
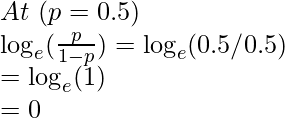
So, at p = 0.5 -> log (odds) = y = 0.
c. At random values
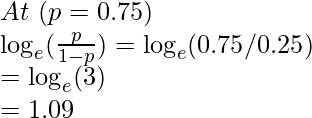
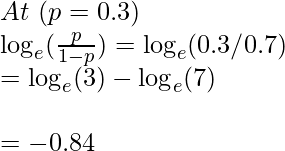
So, at p > 0.5 -> we get value of log(odds) in range (0, ∞)
and at p < 0.5 -> we get value of log(odds) in range (-∞, 0)
If we map these values onto a transformed plot, it would look like: (As shown in Fig 2)
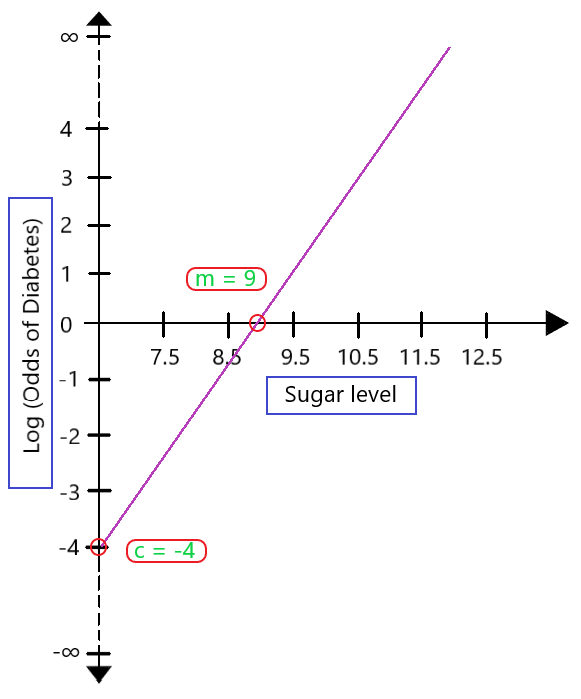
Fig 2 : Transformed LR plot
Based on the value of slope (m) and intercept (c), we can easily interpret the model and get non-binary deterministic output. This is power of log odds in Logistic Regression.
Log odds commonly known as Logit function is used in Logistic Regression models when we are looking non-binary output. This is how logistic regression is able to work as both a regression as well as classification model. For any doubt/query, comment below.
Share your thoughts in the comments
Please Login to comment...