Logistic Regression in R Programming
Last Updated :
05 Jul, 2023
Logistic regression in R Programming is a classification algorithm used to find the probability of event success and event failure. Logistic regression is used when the dependent variable is binary(0/1, True/False, Yes/No) in nature. The logit function is used as a link function in a binomial distribution.
A binary outcome variable’s probability can be predicted using the statistical modeling technique known as logistic regression. It is widely employed in many different industries, including marketing, finance, social sciences, and medical research.
The logistic function, commonly referred to as the sigmoid function, is the basic idea underpinning logistic regression. This sigmoid function is used in logistic regression to describe the correlation between the predictor variables and the likelihood of the binary outcome.

Logistic Regression in R Programming
Logistic regression is also known as Binomial logistics regression. It is based on the sigmoid function where output is probability and input can be from -infinity to +infinity.
Theory
Logistics regression is also known as a generalized linear model. As it is used as a classification technique to predict a qualitative response, the Value of y ranges from 0 to 1 and can be represented by the following equation:

Logistic Regression in R Programming
p is the probability of characteristic of interest. The odds ratio is defined as the probability of success in comparison to the probability of failure. It is a key representation of logistic regression coefficients and can take values between 0 and infinity. The odds ratio of 1 is when the probability of success is equal to the probability of failure. The odds ratio of 2 is when the probability of success is twice the probability of failure. The odds ratio of 0.5 is when the probability of failure is twice the probability of success.

Logistic Regression in R Programming
Since we are working with a binomial distribution(dependent variable), we need to choose a link function that is best suited for this distribution.

Logistic Regression in R Programming
It is a logit function. In the equation above, the parenthesis is chosen to maximize the likelihood of observing the sample values rather than minimizing the sum of squared errors(like ordinary regression). The logit is also known as a log of odds. The logit function must be linearly related to the independent variables. This is from equation A, where the left-hand side is a linear combination of x. This is similar to the OLS assumption that y be linearly related to x. Variables b0, b1, b2 … etc are unknown and must be estimated on available training data. In a logistic regression model, multiplying b1 by one unit changes the logit by b0. The P changes due to a one-unit change will depend upon the value multiplied. If b1 is positive then P will increase and if b1 is negative then P will decrease.
The Dataset
mtcars(motor trend car road test) comprises fuel consumption, performance, and 10 aspects of automobile design for 32 automobiles. It comes pre-installed with dplyr package in R.
R
install.packages("dplyr")
library(dplyr)
summary(mtcars)
|
Performing Logistic regression on a dataset
Logistic regression is implemented in R using glm() by training the model using features or variables in the dataset.
R
install.packages("caTools")
install.packages("ROCR")
library(caTools)
library(ROCR)
|
Splitting the Data
R
split <- sample.split(mtcars, SplitRatio = 0.8)
split
train_reg <- subset(mtcars, split == "TRUE")
test_reg <- subset(mtcars, split == "FALSE")
logistic_model <- glm(vs ~ wt + disp,
data = train_reg,
family = "binomial")
logistic_model
summary(logistic_model)
|
Output:
Call:
glm(formula = vs ~ wt + disp, family = "binomial", data = train_reg)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6552 -0.4051 0.4446 0.6180 1.9191
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.58781 2.60087 0.610 0.5415
wt 1.36958 1.60524 0.853 0.3936
disp -0.02969 0.01577 -1.882 0.0598 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 34.617 on 24 degrees of freedom
Residual deviance: 20.212 on 22 degrees of freedom
AIC: 26.212
Number of Fisher Scoring iterations: 6
- Call: The function call used to fit the logistic regression model is displayed, along with information on the family, formula, and data.
- Deviance Residuals: These are the deviance residuals, which gauge the model’s degree of goodness-of-fit. They stand for discrepancies between actual responses and probability predicted by the logistic regression model.
- Coefficients: These coefficients in logistic regression represent the response variable’s log odds or logit. The standard errors related to the estimated coefficients are shown in the “Std. Error” column.
- Significance codes: The level of significance of each predictor variable is indicated by the significance codes.
- Dispersion parameter: In logistic regression, the dispersion parameter serves as the scaling parameter for the binomial distribution. It is set to 1 in this instance, indicating that the assumed dispersion is 1.
- Null deviance: The null deviance calculates the model’s deviation when just the intercept is taken into account. It symbolizes the deviation that would result from a model with no predictors.
- Residual deviance: The residual deviance calculates the model’s deviation after the predictors have been fitted. It stands for the residual deviation after taking the predictors into account.
- AIC: The Akaike Information Criterion (AIC), which accounts for the number of predictors, is a gauge of a model’s goodness of fit. It penalizes more intricate models in order to prevent overfitting. Better-fitting models are indicated by lower AIC values.
- Number of Fisher Scoring iterations: The number of iterations needed by the Fisher scoring procedure to estimate the model parameters is indicated by the number of iterations.
Predict test data based on model
R
predict_reg <- predict(logistic_model,
test_reg, type = "response")
predict_reg
|
Output:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial
0.01226166 0.78972164 0.26380531 0.01544309
AMC Javelin Camaro Z28 Ford Pantera L
0.06104267 0.02807992 0.01107943
R
predict_reg <- ifelse(predict_reg >0.5, 1, 0)
table(test_reg$vs, predict_reg)
missing_classerr <- mean(predict_reg != test_reg$vs)
print(paste('Accuracy =', 1 - missing_classerr))
ROCPred <- prediction(predict_reg, test_reg$vs)
ROCPer <- performance(ROCPred, measure = "tpr",
x.measure = "fpr")
auc <- performance(ROCPred, measure = "auc")
auc <- auc@y.values[[1]]
auc
plot(ROCPer)
plot(ROCPer, colorize = TRUE,
print.cutoffs.at = seq(0.1, by = 0.1),
main = "ROC CURVE")
abline(a = 0, b = 1)
auc <- round(auc, 4)
legend(.6, .4, auc, title = "AUC", cex = 1)
|
Output:

ROC Curve
Example 2:
We can perform a logistic regression model Titanic Data set in R.
R
data(Titanic)
data <- as.data.frame(Titanic)
model <- glm(Survived ~ Class + Sex + Age, family = binomial, data = data)
summary(model)
|
Output:
Call:
glm(formula = Survived ~ Class + Sex + Age, family = binomial,
data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.177 -1.177 0.000 1.177 1.177
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.022e-16 8.660e-01 0 1
Class2nd -9.762e-16 1.000e+00 0 1
Class3rd -4.699e-16 1.000e+00 0 1
ClassCrew -5.551e-16 1.000e+00 0 1
SexFemale -3.140e-16 7.071e-01 0 1
AgeAdult 5.103e-16 7.071e-01 0 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 44.361 on 31 degrees of freedom
Residual deviance: 44.361 on 26 degrees of freedom
AIC: 56.361
Number of Fisher Scoring iterations: 2
Plot the ROC curve for the Titanic data set
R
install.packages("ROCR")
library(ROCR)
model <- glm(Survived ~ Class + Sex + Age, family = binomial, data = data)
predictions <- predict(model, type = "response")
prediction_objects <- prediction(predictions, titanic_df$Survived)
roc_object <- performance(prediction_obj, measure = "tpr", x.measure = "fpr")
plot(roc_object, main = "ROC Curve", col = "blue", lwd = 2)
legend("bottomright", legend =
paste("AUC =", round(performance(prediction_objects, measure = "auc")
@y.values[[1]], 2)), col = "blue", lwd = 2)
|
Output:
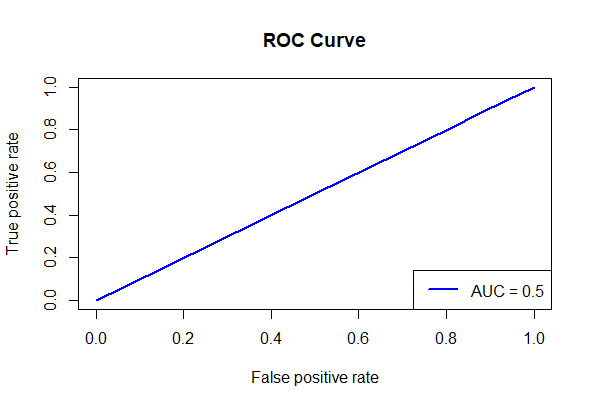
ROC curve
- The factors used to predict “Survived” are specified, and the formula Survived Class + Sex + Age is used to create a logistic regression model.
- Using the predict() function, predictions are made on the dataset using the fitted model.
- The projected probabilities are combined with the actual outcome values to build a prediction object using the prediction() method from the ROCR package.
- The measure of the true positive rate (tpr) and the x-axis measure of the false positive rate (fpr) are specified, and a ROC curve object is created using the performance() function from the ROCR package.
- The ROC curve object (roc_obj), which specifies the main title, color, and line width, is plotted using the plot() function.
- It uses the performance() function with measure = “auc” to determine the AUC (area under the curve) value and adds labels and a legend to the plot.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...