Puzzle | Number of Sheets to be turned so that Prime Number has a Vowel on the other side
Last Updated :
18 Jan, 2023
There are five sheets of paper each of which has a whole number on one side and an alphabet on the other side written on it as shown below. 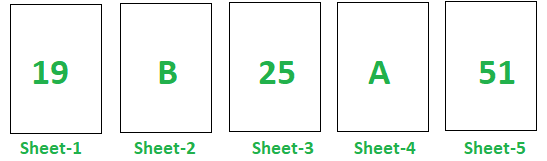
What is the minimum number of sheets that is necessary and sufficient that you will turn over to verify whether the proposition given below about them is true or false? What are the sheets that you will turn over?
Proposition: “If there is a prime number on one side of a sheet then the other side of the sheet has a vowel.”
Answer: Two: Sheets 1 and 2.
Solution: Sheet 1 has to be turned over to verify the truth of the proposition. If it doesn’t contain a vowel on the other side, then the proposition can be declared as false. This will verify the statement to be true. Sheet 2 has also to be turned over. If it has got a prime number on the other side then it will disprove the proposition. This will verify the statement to generally true for all cases by the help of contradiction. One does not need to turn over sheet 4 because the proposition doesn’t imply that only those sheets with a prime number on one side have got a vowel on the other. Sheets 3 and 5 are of no help to disprove or prove the proposition obviously.
Share your thoughts in the comments
Please Login to comment...