Proof that Path Selection Decision problem is NP-Complete
Last Updated :
16 Jun, 2020
Prerequisite –
NP-Completeness
The decision problem of path selection problem asks if it is possible to select at least k paths from the given paths of a graph such that no two selected paths share any vertex.
To prove that a problem is NP-Complete, we need to show that it is both NP and NP-Hard. We use PSP to denote our path selection decision problem.
The PSP belongs to NP :
We prove this by constructing a polynomial time verifier for the problem. If any problem is in NP, then, given a ‘certificate’ (a solution) to the problem and an instance of the problem (a graph G and a positive integer k, in this case), we will be able to verify (check whether the solution given is correct or not) the certificate in polynomial time.
The certificate for PSP is a set of paths P’. These are independent paths with no common edges. We can check whether there are k paths which are independent for the given a graph G(V, E)) and paths P in the following manner:
Check if P' is a subset of P
If not, the given solution is wrong
The number of paths in P' is at least k
If not, the given solution is wrong
Initialize a list of boolean with length |V|
for each path p in P'
for each vertex in p
check if it is marked True in our list
If so, the given solution is wrong
Else, marks the vertex as True
Since no vertex was marked twice,
given solution is correct.
The above verifier is polytime since:
- Checking P’ is a subset of P can be done in O(|P|).
- Checking number of paths in P’ can be done in O(|P’|)
- Checking all the paths are disjoint can be done in O(|V|)
Hence, total time complexity :
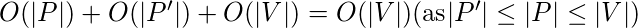
Therefore, the PSP has polynomial time verifiability and hence belongs to the NP Class.
The Clique Decision Problem belongs to NP-Hard :
To prove that PSP is NP Hard, we take some problem which has already been proven to be NP Hard (Independent Set in our case), and show that this problem can be reduced to the PSP in polynomial time. Since we know Independent set is NP complete, hence it is also NP hard.
Given a IS instance –
G=(V, E) and k
We construct the PSP instance in the following manner:
We create a new graph G’. For every vertex v
i in G:
- We denote a path by Pi for vi.
- Let e1, e2, …, er be the edges connected to vi. We introduce a vertex for each such edge in G’. Further, we introduce a pair of vertices in G’ – si, ti.
Thus,
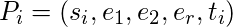
We can clearly see that the above reduction is polytime(with complexity = O(|V|+|E|)) as we are essentially iterating over all the vertex and the edges in our initial graph.
Proof :
Proof that the Independent Set problem reduces to the Path Selection Problem. To prove that our reduction is correct we prove the following two arguments.
(i) YES, instance for IS => Yes instance for PSP
We have, YES instance for IS.
- For a graph G=(V, E) there exist an independent set of size at least k.
- There exist at least k vertices that don’t share any edge.
- There exist at least k paths that don’t share any node in the instance of PSP. Since we are defining the vertices of G to be analogous to paths in the instance of PSP and edges of G to be analogous to vertices in those paths. And any of these path sharing nodes would mean that some two vertices in the independent set share a common edge which is never possible.
- Yes, instance for PSP.
(ii) YES, instance for PSP => Yes instance for IS
ETP: No instance for IS => No instance for PSP. (Proof by contrapositive.).
We know that whenever there exist an independent set of size at least k, there exist an independent set of size exactly k(This can be done by taking the subset of size k from the bigger set). Hence, the contrapositive is also true. (i.e, Whenever there cannot exist an independent set of size exactly k, there cannot exist an independent set of size at least k).
We have No instance of IS.
- For a graph G=(V, E) there cannot exist an independent set of size k.
- It is not possible to find k vertices of G that don’t share any edge.
- Every set S of vertices of size k would contain vi and vj that share an edge.
- Since we are defining the vertices of G to be analogous to paths in the instance of PSP and edges of G to be analogous to vertices in those paths, every k size set of Paths in instance of PSP would share a node.
- There cannot exist k paths that don’t share any node in the instance of PSP.
- No instance for PSP.
Hence, for a particular instance, the IS problem is reduced to the PSP. Therefore PSP is NP-Hard.
Thus, The Path Selection Decision Problem is NP and NP-Hard. Therefore, the Path Selection Decision problem is NP-Complete.
Share your thoughts in the comments
Please Login to comment...