Proof that Hamiltonian Path is NP-Complete
Last Updated :
29 Mar, 2023
Prerequisite : NP-Completeness The class of languages for which membership can be decided quickly fall in the class of P and The class of languages for which membership can be verified quickly fall in the class of NP(stands for problem solved in Non-deterministic Turing Machine in polynomial time). In straight words, every NP problem has its own polynomial-time verifier. A verifier for a language A is an algorithm V, where
A = {w | V accepts (w, c) for some string c}
where c is certificate or proof that w is a member of A.
We are interested in NP-Complete problems. NP-Complete problem is defined as follows:
(1)The problem itself is in NP class.
(2)All other problems in NP class can be polynomial time reducible to that.
(B is polynomial time reducible to C is denoted as 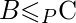 )
)
If the 2nd condition is only satisfied then the problem is called NP-Hard. But it is not possible to reduce every NP problem into another NP problem to show its NP-Completeness all the time. That is why if we want to show a problem is NP-Complete we just show that the problem is in NP and any NP-Complete problem is reducible to that then we are done, i.e. if B is NP-Complete and 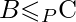 for C in NP, then C is NP-Complete. We have to show Hamiltonian Path is NP-Complete. Hamiltonian Path or HAMPATH in a directed graph G is a directed path that goes through each node exactly once. We Consider the problem of testing whether a directed graph contain a Hamiltonian path connecting two specified nodes, i.e.
for C in NP, then C is NP-Complete. We have to show Hamiltonian Path is NP-Complete. Hamiltonian Path or HAMPATH in a directed graph G is a directed path that goes through each node exactly once. We Consider the problem of testing whether a directed graph contain a Hamiltonian path connecting two specified nodes, i.e.
HAMPATH = {(G, s, t) | G is directed graph with a Hamiltonian path from s to t}
To prove HAMPATH is NP-Complete we have to prove that HAMPATH is in NP. To prove HAMPATH is in NP we must have a polynomial-time verifier. Even though we don’t have a fast polynomial time algorithm to determine whether a graph contains a HAMPATH or not, if such a path is discovered somehow (maybe with exponential time brute force searching) we could easily-work it out whether the path is HAMPATH or not, in polynomial time. Here the certificate will be a Hamiltonian path from s to t itself in G if exists. So HAMPATH is in NP proved. So, now we have to show that every problem to NP class is polynomial time reducible to HAMPATH to show its NP-Completeness. Rather we shall show 3SAT (A NP-Complete problem proved previously from SAT(Circuit Satisfiability Problem)) is polynomial time reducible to HAMPATH. We will convert a given cnf (Conjunctive Normal Form) form to a graph where gadgets (structure to simulate variables and clauses) will mimic the variables and clauses (several literals or variables connected with  ). We have to prove now
). We have to prove now 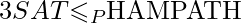 For each 3-cnf formula
For each 3-cnf formula 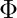 we will show how to build graph G with s and t, where a Hamiltonian path exists between s and t if
we will show how to build graph G with s and t, where a Hamiltonian path exists between s and t if 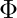 is satisfiable. We start with a 3-cnf formula
is satisfiable. We start with a 3-cnf formula 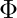 containing k clauses,
containing k clauses,
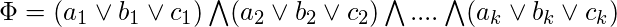
where each 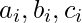 is a literal
is a literal 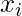 or
or 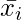 . Let
. Let 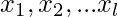 be the l variables of
be the l variables of 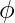 .Now we show how to convert
.Now we show how to convert 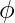 to a graph G. The graph G that we construct has various parts to represent the variables and clauses that appear in
to a graph G. The graph G that we construct has various parts to represent the variables and clauses that appear in 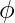 . We represent each variable
. We represent each variable 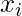 with a diamond-shaped structure that contains a horizontal row of nodes as shown in following figure. We specify the number of nodes that appear in the horizontal row later.
with a diamond-shaped structure that contains a horizontal row of nodes as shown in following figure. We specify the number of nodes that appear in the horizontal row later.

The following figure depicts the global structure of G. It shows all the elements of G and their relationships, except the edges that represent the relationship of the variables to the clauses that contain them.
 Each diamond structure contains a horizontal row of nodes connected by edges running in both directions. The horizontal row contains 2k nodes (as 2 nodes for each clause) plus, k-1 extra nodes in between every two nodes for a clause plus, 2 nodes on the ends belonging to the diamonds; total 3k+1 nodes. Following diagram gives a clear picture.
Each diamond structure contains a horizontal row of nodes connected by edges running in both directions. The horizontal row contains 2k nodes (as 2 nodes for each clause) plus, k-1 extra nodes in between every two nodes for a clause plus, 2 nodes on the ends belonging to the diamonds; total 3k+1 nodes. Following diagram gives a clear picture.

If variable 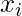 appears in clause
appears in clause 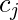 , we add the following two edges from the jth pair in the ith diamond to the jth clause node.
, we add the following two edges from the jth pair in the ith diamond to the jth clause node.
 If
If 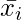 appears in clause c_j, we add two edges from the jth pair in the ith diamond to the jth clause node, as in the following figure.
appears in clause c_j, we add two edges from the jth pair in the ith diamond to the jth clause node, as in the following figure.

After we add all the edges corresponding to each occurrence of 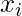 or
or 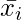 in each clause, the construction of G is complete. To show its correctness we will prove if
in each clause, the construction of G is complete. To show its correctness we will prove if 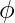 is satisfiable, a Hamiltonian path exists from s to t and conversely, if such a path exists
is satisfiable, a Hamiltonian path exists from s to t and conversely, if such a path exists 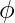 is satisfiable. Suppose that
is satisfiable. Suppose that 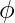 is satisfiable. To demonstrate a Hamiltonian path from s to t, we first ignore the clause nodes. The path begins at s, goes through each diamond in turn and ends up at t. To hit horizontal nodes in a diamond. the path either zig-zags from left to right or zag-zigs from right to left; the satisfying assignment to
is satisfiable. To demonstrate a Hamiltonian path from s to t, we first ignore the clause nodes. The path begins at s, goes through each diamond in turn and ends up at t. To hit horizontal nodes in a diamond. the path either zig-zags from left to right or zag-zigs from right to left; the satisfying assignment to 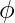 determines whether
determines whether 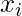 is assigned TRUE or FALSE respectively. We show both cases in the following figure.
is assigned TRUE or FALSE respectively. We show both cases in the following figure.

So far this path covers all the nodes in G except the clause nodes. We can easily include them by adding detours at the horizontal nodes. In each clause, we select one of the literals assigned TRUE, by satisfying assignment. If we selected 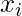 in clause
in clause 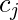 , we can detour at the jth pair in the ith diamond. Doing so is possible because
, we can detour at the jth pair in the ith diamond. Doing so is possible because 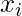 must be TRUE, so the path zig-zags from left to right through the corresponding diamond. Hence the edges to the
must be TRUE, so the path zig-zags from left to right through the corresponding diamond. Hence the edges to the 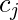 node are in the correct order to allow a detour and return. Similarly, if we selected
node are in the correct order to allow a detour and return. Similarly, if we selected 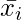 in clause
in clause 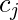 , we can detour at the jth pair in the ith diamond because
, we can detour at the jth pair in the ith diamond because 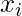 must be FALSE, so the path zag-zigs from right to left through the corresponding diamond. Hence the edges to the
must be FALSE, so the path zag-zigs from right to left through the corresponding diamond. Hence the edges to the 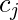 node are again in the correct order to allow a detour and return. Every time one detour is taken if each literal in clause provides an option for detour. Thus each node is visited exactly once and thus Hamiltonian Path is constructed. For the reverse direction, if G has a Hamiltonian path from s to t, we demonstrate a satisfying assignment for
node are again in the correct order to allow a detour and return. Every time one detour is taken if each literal in clause provides an option for detour. Thus each node is visited exactly once and thus Hamiltonian Path is constructed. For the reverse direction, if G has a Hamiltonian path from s to t, we demonstrate a satisfying assignment for 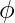 . If the Hamiltonian path is normal i.e. it goes through diamonds in order from top to bottom node except the detour for the closure nodes; we can easily obtain the satisfying assignment. If the path zig-zags in diamond we assign the variables as TRUE and if it zag-zigs then assign it FALSE. Because every node appears on the path by observing how the detour is taken we may determine corresponding TRUE variables. All that remains to be shown that Hamiltonian path must be normal means the path enters a clause from one diamond but returns to another like in the following figure.
. If the Hamiltonian path is normal i.e. it goes through diamonds in order from top to bottom node except the detour for the closure nodes; we can easily obtain the satisfying assignment. If the path zig-zags in diamond we assign the variables as TRUE and if it zag-zigs then assign it FALSE. Because every node appears on the path by observing how the detour is taken we may determine corresponding TRUE variables. All that remains to be shown that Hamiltonian path must be normal means the path enters a clause from one diamond but returns to another like in the following figure.

The path goes from node 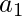 to c; but instead of returning to
to c; but instead of returning to 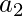 in the same diamond, it returns to
in the same diamond, it returns to 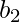 in the different diamond. If that occurs then either
in the different diamond. If that occurs then either 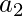 or
or 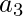 must be a separator node. If
must be a separator node. If 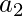 were a separator node, the only edges entering in
were a separator node, the only edges entering in 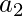 would be from
would be from 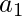 or
or 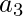 . If
. If 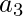 were a separator node then
were a separator node then 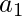 and
and 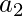 would be in same clause, then edges that enters
would be in same clause, then edges that enters 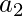 from
from 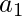 ,
, 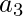 and c. In either case path cannot enter
and c. In either case path cannot enter 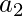 from
from 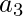 because
because 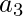 is only available node that
is only available node that 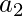 points at, so path must exit
points at, so path must exit 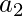 via
via 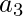 . Hence Hamiltonian path must be normal. This reduction obviously operates in polynomial time and hence the proof is complete that HAMPATH is NP-Complete.
. Hence Hamiltonian path must be normal. This reduction obviously operates in polynomial time and hence the proof is complete that HAMPATH is NP-Complete.
Share your thoughts in the comments
Please Login to comment...