Program to print pentatope numbers upto Nth term
Last Updated :
25 May, 2022
Prerequisites:
Given a value n, and the task is to print pentatope numbers series up to nth term.
Examples:
Input: 5
Output: 1 5 15 35 70
Input: 10
Output: 1 5 15 35 70 126 210 330 495 715
Method 1: Using Tetrahedral Number Series:
This problem can be easily solved with the fact that Nth Pentatope Number is equal to the sum of first N Tetrahedral numbers.
Let’s have a look on Series of Pentatope and Tetrahedral Numbers.
For n = 5
Tetrahedral Numbers = 1, 4, 10, 20, 35
Prefix Sum of Tetrahedral numbers for each term: (1), (1 + 4), (1 + 4 + 10), (1 + 4 + 10 + 20), (1 + 4 + 10 + 20 + 35)
So, Pentatope numbers are 1, 5, 15, 35, 70
Calculate Nth Tetrahedral number using formula: 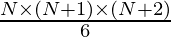
So, print the Pentatope Numbers series by generating tetrahedral numbers and adding it with the sum of all previously generated Tetrahedral Numbers.
Below is the implementation of above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
int findTetrahedralNumber(int n)
{
return ((n * (n + 1) * (n + 2)) / 6);
}
void printSeries(int n)
{
int prev = 0;
int curr;
for (int i = 1; i <= n; i++)
{
curr = findTetrahedralNumber(i);
curr = curr + prev;
cout << curr << " ";
prev = curr;
}
}
int main()
{
int n = 10;
printSeries(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int findTetrahedralNumber(int n)
{
return ((n * (n + 1) * (n + 2)) / 6);
}
static void printSeries(int n)
{
int prev = 0;
int curr;
for (int i = 1; i <= n; i++)
{
curr = findTetrahedralNumber(i);
curr = curr + prev;
System.out.print(curr + " ");
prev = curr;
}
}
public static void main (String[] args)
{
int n = 10;
printSeries(n);
}
}
|
python3
def findTetrahedralNumber(n) :
return (int((n * (n + 1) * (n + 2)) / 6))
def printSeries(n) :
prev = 0
for i in range(1, n + 1) :
curr = findTetrahedralNumber(i)
curr = curr + prev;
print(curr, end=' ')
prev = curr
n = 10
printSeries(n)
|
C#
using System;
public class GFG {
static int findTetrahedralNumber(int n)
{
return ((n * (n + 1) * (n + 2)) / 6);
}
static void printSeries(int n)
{
int prev = 0;
int curr;
for (int i = 1; i <= n; i++)
{
curr = findTetrahedralNumber(i);
curr = curr + prev;
Console.Write(curr + " ");
prev = curr;
}
}
static public void Main ()
{
int n = 10;
printSeries(n);
}
}
|
PHP
<?php
function findTetrahedralNumber($n)
{
return (($n * ($n + 1) * ($n + 2)) / 6);
}
function printSeries($n)
{
$prev = 0;
$curr;
for ($i = 1; $i <= $n; $i++)
{
$curr = findTetrahedralNumber($i);
$curr = $curr + $prev;
echo($curr . " ");
$prev = $curr;
}
}
$n = 10;
printSeries($n);
?>
|
Javascript
<script>
function findTetrahedralNumber(n)
{
return ((n * (n + 1) * (n + 2)) / 6);
}
function printSeries(n)
{
let prev = 0;
let curr;
for (let i = 1; i <= n; i++)
{
curr = findTetrahedralNumber(i);
curr = curr + prev;
document.write(curr+" ");
prev = curr;
}
}
let n = 10;
printSeries(n);
</script>
|
Output: 1 5 15 35 70 126 210 330 495 715
Time Complexity: O(n), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Method 2: Using Pentatope Number Formula:
The formula to find Nth Pentatope number 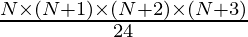
Below is the required implementation:
CPP
#include <bits/stdc++.h>
using namespace std;
void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = (i * (i + 1) * (i + 2) * (i + 3) / 24);
cout << num << " ";
}
}
int main()
{
int n = 10;
printSeries(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = (i * (i + 1) * (i + 2) * (i + 3) / 24);
System.out.print(num + " ");
}
}
public static void main (String[] args)
{
int n = 10;
printSeries(n);
}
}
|
python3
def printSeries(n) :
for i in range(1, n + 1) :
num = int(i * (i + 1) * (i + 2) * (i + 3) // 24)
print(num, end=' ');
n = 10
printSeries(n)
|
C#
using System;
public class GFG {
static void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = (i * (i + 1) * (i + 2) * (i + 3) / 24);
Console.Write(num + " ");
}
}
static public void Main ()
{
int n = 10;
printSeries(n);
}
}
|
PHP
<?php
function printSeries($n)
{
for ($i = 1; $i <= $n; $i++)
{
$num = ($i * ($i + 1) * ($i + 2) * ($i + 3) / 24);
echo($num . " ");
}
}
$n = 10;
printSeries($n);
?>
|
Javascript
<script>
function printSeries(n)
{
for (let i = 1; i <= n; i++)
{
num = (i * (i + 1) * (i + 2) * (i + 3) / 24);
document.write(num+" ");
}
}
let n = 10;
printSeries(n);
</script>
|
Output: 1 5 15 35 70 126 210 330 495 715
Time Complexity: O(n), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...