Program for sum of cosh(x) series upto Nth term
Last Updated :
25 May, 2022
Given two numbers x and N, the task is to find the value of cosh(x) from the series upto N terms.
The expansion of cosh(x) is given below:
cosh(x) = 1 + x2/2! + x4/4! + …………
Examples:
Input: x = 1, N = 5
Output: 1.54308035714
Input: x = 1, N = 10
Output: 1.54308063497
Approach:
The above series can be easily implemented using a factorial function and loops.
The nth term of the series is:
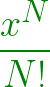
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int fact(int n)
{
int i = 1, fac = 1;
for (i = 1; i <= n; i++)
fac = fac * i;
return fac;
}
double log_Expansion(double x, int n)
{
double sum = 0;
int i = 0;
for (i = 0; i < n; i++) {
sum = sum
+ pow(x, 2 * i)
/ fact(2 * i);
}
return sum;
}
int main()
{
double x = 1;
int n = 10;
cout << setprecision(12)
<< log_Expansion(x, n)
<< endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int fact(int n)
{
int i = 1, fac = 1;
for (i = 1; i <= n; i++)
fac = fac * i;
return fac;
}
static double log_Expansion(double x, int n)
{
double sum = 0;
int i = 0;
for (i = 0; i < n; i++)
{
sum = sum + Math.pow(x, 2 * i) /
fact(2 * i);
}
return sum;
}
public static void main(String[] args)
{
double x = 1;
int n = 10;
System.out.println(log_Expansion(x, n));
}
}
|
Python3
def fact(n):
i, fac = 1, 1
for i in range(1, n + 1):
fac = fac * i
return fac
def log_Expansion(x, n):
Sum = 0
i = 0
for i in range(n):
Sum = Sum + pow(x, 2 * i) / fact(2 * i)
return Sum
x = 1
n = 10
print(log_Expansion(x, n))
|
C#
using System;
class GFG
{
static int fact(int n)
{
int i = 1, fac = 1;
for (i = 1; i <= n; i++)
fac = fac * i;
return fac;
}
static double log_Expansion(double x, int n)
{
double sum = 0;
int i = 0;
for (i = 0; i < n; i++)
{
sum = sum + Math.Pow(x, 2 * i) /
fact(2 * i);
}
return sum;
}
public static void Main(String[] args)
{
double x = 1;
int n = 10;
Console.WriteLine(log_Expansion(x, n));
}
}
|
Javascript
<script>
function fact( n) {
let i = 1, fac = 1;
for (i = 1; i <= n; i++)
fac = fac * i;
return fac;
}
function log_Expansion( x , n) {
let sum = 0;
let i = 0;
for (i = 0; i < n; i++) {
sum = sum + Math.pow(x, 2 * i) / fact(2*i);
}
return sum;
}
let x = 1;
let n = 10;
document.write(log_Expansion(x, n).toFixed(11));
</script>
|
Time Complexity: O(n2), where n represents the value of the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...