Program to print tetrahedral numbers upto Nth term
Last Updated :
25 May, 2022
Prerequisites:
Given a value n, and the task is to print tetrahedral number series up to nth term.
Examples:
Input: 5
Output: 1 4 10 20 35
Input: 10
Output: 1 4 10 20 35 56 84 120 165 220
Method 1: Using Triangular Number series:
This problem can be easily solved with the fact that Nth Tetrahedral Number is equal to the sum of first N Triangular Numbers.
Let’s have a look on Series of triangular and tetrahedral Numbers.
To print series upto 5th term:
Triangular Numbers = 1 3 6 10 15
Tetrahedral numbers = 1 4 10 20 35
i.e (1) (1 + 3) (1 + 3 + 6) (1 + 3 + 6 + 10) (1 + 3 + 6 + 10 + 35)
Calculate Nth Triangular number using formula 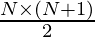
So, print the tetrahedral numbers series by generating triangular numbers and adding it with the sum of all previously generated triangular numbers.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long findTriangularNumber(int n)
{
return (n * (n + 1)) / 2;
}
void printSeries(int n)
{
int prev = 0;
int curr;
for (int i = 1; i <= n; i++)
{
curr = findTriangularNumber(i);
curr = curr + prev;
cout << curr << " ";
prev = curr;
}
}
int main()
{
int n = 10;
printSeries(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static long findTriangularNumber(int n)
{
return (n * (n + 1)) / 2;
}
static void printSeries(int n)
{
long prev = 0;
long curr;
for (int i = 1; i <= n; i++)
{
curr = findTriangularNumber(i);
curr = curr + prev;
System.out.print(curr + " ");
prev = curr;
}
}
public static void main (String[] args)
{
int n = 10;
printSeries(n);
}
}
|
Python3
def findTriangularNumber(n):
return (n * (n + 1)) / 2
def printSeries(n):
prev = 0
for i in range(1, n+1):
curr = findTriangularNumber(i)
curr = int(curr + prev)
print(curr, end = ' ')
prev = curr
n = 10
printSeries(n)
|
C#
using System;
public class GFG{
static long findTriangularNumber(int n)
{
return (n * (n + 1)) / 2;
}
static void printSeries(int n)
{
long prev = 0;
long curr;
for (int i = 1; i <= n; i++)
{
curr = findTriangularNumber(i);
curr = curr + prev;
Console.Write(curr + " ");
prev = curr;
}
}
static public void Main ()
{
int n = 10;
printSeries(n);
}
}
|
PHP
<?php
function findTriangularNumber($n)
{
return ($n * ($n + 1)) / 2;
}
function printSeries($n)
{
$prev = 0;
$curr;
for ($i = 1; $i <= $n; $i++)
{
$curr = findTriangularNumber($i);
$curr = $curr + $prev;
echo($curr . " ");
$prev = $curr;
}
}
$n = 10;
printSeries($n);
?>
|
Javascript
<script>
function findTriangularNumber(n)
{
return (n * (n + 1)) / 2;
}
function printSeries(n)
{
var prev = 0;
var curr;
for (var i = 1; i <= n; i++)
{
curr = findTriangularNumber(i);
curr = curr + prev;
document.write( curr + " ");
prev = curr;
}
}
var n = 10;
printSeries(n);
</script>
|
Output: 1 4 10 20 35 56 84 120 165 220
Time Complexity: O(n), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Method 2: Using Tetrahedral Number Formula:
Formula to find nth tetrahedral number: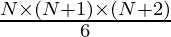
Below is the required implementation:
C++
#include <bits/stdc++.h>
using namespace std;
void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = i * (i + 1) * (i + 2) / 6;
cout << num << " ";
}
}
int main()
{
int n = 10;
printSeries(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = i * (i + 1) * (i + 2) / 6;
System.out.print(num + " ");
}
}
public static void main (String[] args)
{
int n = 10;
printSeries(n);
}
}
|
Python3
def printSeries(n):
for i in range(1, n + 1):
num = i * (i + 1) * (i + 2) // 6
print(num, end =' ')
n = 10
printSeries(n)
|
C#
using System;
public class GFG{
static void printSeries(int n)
{
for (int i = 1; i <= n; i++)
{
int num = i * (i + 1) * (i + 2) / 6;
Console.Write(num + " ");
}
}
static public void Main ()
{
int n = 10;
printSeries(n);
}
}
|
PHP
<?php
function printSeries($n)
{
for ($i = 1; $i <= $n; $i++)
{
$num = $i * ($i + 1) * ($i + 2) / 6;
echo ($num . " ");
}
}
$n = 10;
printSeries($n);
?>
|
Javascript
<script>
function printSeries(n)
{
let i;
for (i = 1; i <= n; i++)
{
let num = i * (i + 1) * ((i + 2) / 6);
document.write(num + " ");
}
}
let n = 10;
printSeries(n);
</script>
|
Output: 1 4 10 20 35 56 84 120 165 220
Time Complexity: O(n), where n represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...