Program to check if N is a Enneadecagonal Number

Last Updated : 12 Apr, 2021

Given a number N, the task is to check if N is a Enneadecagonal Number or not. If the number N is an Enneadecagonal Number then print “Yes” else print “No”.

Enneadecagonal Number is a 19-sided polygon in mathematics. It belongs to a class of figurative number. The number contains the number of dots and the dots are arranged in a pattern or series. An Enneadecagonal Number is also known as Nonadecagon. The dots have common points and all other dots are arrange in the successive layer. The nth Enneadecagonal Number counts the seventeen number of dots and all the other dots are surrounding with a common sharing corner and make a pattern. The first few Enneadecagonal Numbers are 1, 19, 54, 106, 175…
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.
In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

Examples:

Input: N = 19
Output: Yes
Explanation:
Second Enneadecagonal Number is 19.
Input: N = 30
Output: No

Approach:

1. The K^th term of the Enneadecagonal Number is given as
$K^{th} Term = \frac{17*K^{2} - 15*K}{2}$

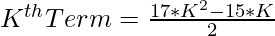
2. As we have to check that the given number can be expressed as a Enneadecagonal Number or not. This can be checked as:

=> $N = \frac{17*K^{2} - 15*K}{2}$
=> $K = \frac{15 + \sqrt{136*N + 225}}{34}$

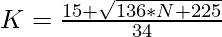
3. If the value of K calculated using the above formula is an integer, then N is a Enneadecagonal Number.

4. Else N is not a Enneadecagonal Number.

Below is the implementation of the above approach:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to check if number N
// is a enneadecagonal number
bool isenneadecagonal(int N)
{
    float n
        = (15 + sqrt(136 * N + 225))
          / 34;
 
    // Condition to check if N is a
    // enneadecagonal number
    return (n - (int)n) == 0;
}
 
// Driver Code
int main()
{
    // Given Number
    int N = 19;
 
    // Function call
    if (isenneadecagonal(N)) {
        cout << "Yes";
    }
    else {
        cout << "No";
    }
    return 0;
}

Java

// Java program for the above approach
class GFG{
 
// Function to check if number N
// is a enneadecagonal number
static boolean isenneadecagonal(int N)
{
    float n = (float)(15 + Math.sqrt(136 * N +
                                     225)) / 34;
 
    // Condition to check if N is a
    // enneadecagonal number
    return (n - (int)n) == 0;
}
 
// Driver Code
public static void main(String[] args)
{
     
    // Given Number
    int N = 19;
 
    // Function call
    if (isenneadecagonal(N))
    {
        System.out.println("Yes");
    }
    else
    {
        System.out.println("No");
    }
}
}
 
// This code is contributed by rutvik_56

Python3

# Python3 program for the above approach
import math
 
# Function to check if number N
# is a enneadecagonal number
def isenneadecagonal(N):
 
    n = (15 + math.sqrt(136 * N + 225)) / 34
 
    # Condition to check if N is a
    # enneadecagonal number
    return (n - int(n)) == 0
 
# Driver Code
N = 19
 
# Function call
if (isenneadecagonal(N)):
    print("Yes")
else:
    print("No")
 
# This code is contributed by divyamohan123

C#

// C# program for the above approach
using System;
 
class GFG{
 
// Function to check if number N
// is a enneadecagonal number
static bool isenneadecagonal(int N)
{
    float n = (float)(15 + Math.Sqrt(136 * N +
                                     225)) / 34;
     
    // Condition to check if N is a
    // enneadecagonal number
    return (n - (int)n) == 0;
}
     
// Driver Code
static public void Main ()
{
         
    // Given number
    int N = 19;
     
    // Function call
    if (isenneadecagonal(N))
    {
        Console.Write("Yes");
    }
    else
    {
        Console.Write("No");
    }
}
}
 
// This code is contributed by shubhamsingh10

Javascript

<script>
 
// Javascript program for the above approach
 
 
// Function to check if number N
// is a enneadecagonal number
function isenneadecagonal(N){
 
    let n = parseFloat(15 + Math.sqrt(136 * N + 225)) / 34;
 
    // Condition to check if N is a
    //enneadecagonal number
    return (n - parseInt(n)) == 0
}
// Driver Code
let N = 19;
 
// Function call
 
if (isenneadecagonal(N)){
    document.write("Yes");
    }
else{
    document.write("No");
    }
 
// This code is contributed by bobby
 
</script>

Output:

Yes

Time Complexity: O(1)

Auxiliary Space: O(1)

My Personal Notes

Related Articles

Related Articles

Program to check if N is a Enneadecagonal Number

C++

Java

Python3

C#

Javascript