Program to calculate the value of sin(x) and cos(x) using Expansion
Last Updated :
16 Feb, 2023
Given a value of angle, you need to calculate Sin and Cos values corresponding to it.
For sin function
Examples:
Input : 90
Output : 1
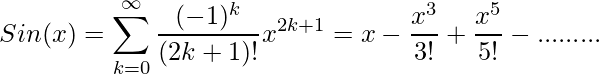
C++
#include <iostream>
#include <math.h>
using namespace std;
void cal_sin(float n)
{
float accuracy = 0.0001, denominator, sinx, sinval;
n = n * (3.142 / 180.0);
float x1 = n;
sinx = n;
sinval = sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= fabs(sinval - sinx));
cout << sinx;
}
int main()
{
float n = 90;
cal_sin(n);
return 0;
}
|
Java
import static java.lang.Math.sin;
class GFG {
static void cal_sin(float n)
{
float accuracy = (float) 0.0001, denominator, sinx, sinval;
n = n * (float)(3.142 / 180.0);
float x1 = n;
sinx = n;
sinval = (float)sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= sinval - sinx);
System.out.println(sinx);
}
public static void main(String[] args) {
float n = 90;
cal_sin(n);
}
}
|
Python3
import math;
def cal_sin(n):
accuracy = 0.0001;
n = n * (3.142 / 180.0);
x1 = n;
sinx = n;
sinval = math.sin(n);
i = 1;
while(True):
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
if(accuracy <= abs(sinval - sinx)):
break;
print(round(sinx));
n = 90;
cal_sin(n);
|
C#
using System;
class GFG
{
static void cal_sin(float n)
{
float accuracy = (float) 0.0001,
denominator, sinx, sinval;
n = n * (float)(3.142 / 180.0);
float x1 = n;
sinx = n;
sinval = (float)Math.Sin(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = sinx + x1;
i = i + 1;
} while (accuracy <= sinval - sinx);
Console.WriteLine(sinx);
}
static public void Main ()
{
float n = 90;
cal_sin(n);
}
}
|
PHP
<?php
function cal_sin($n)
{
$accuracy = 0.0001;
$n = $n * (3.142 / 180.0);
$x1 = $n;
$sinx = $n;
$sinval = sin($n);
$i = 1;
do
{
$denominator = 2 * $i * (2 * $i + 1);
$x1 = -$x1 * $n * $n / $denominator;
$sinx = $sinx + $x1;
$i = $i + 1;
} while ($accuracy <= abs($sinval - $sinx));
echo round($sinx);
}
$n = 90;
cal_sin($n);
?>
|
Javascript
<script>
function cal_sin(n) {
var accuracy = 0.0001, denominator, sinx, sinval;
n = n * (3.142 / 180.0);
var x1 = n;
sinx = n;
sinval = Math.sin(n);
var i = 1;
do {
denominator = 2 * i * (2 * i + 1);
x1 = -x1 * n * n / denominator;
sinx = (sinx + x1);
i = i + 1;
} while (accuracy <= sinval - sinx);
document.write(sinx.toFixed(0));
}
var n = 90;
cal_sin(n);
</script>
|
Output:
1
Time Complexity: O(n)
Space Complexity: O(1)
For cos function
Examples:
Input : 30
Output : 0.86602
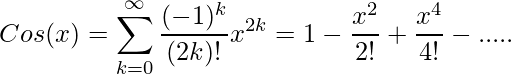
C++
#include <iostream>
#include <math.h>
using namespace std;
void cal_cos(float n)
{
float accuracy = 0.0001, x1, denominator, cosx, cosval;
n = n * (3.142 / 180.0);
x1 = 1;
cosx = x1;
cosval = cos(n);
int i = 1;
do
{
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= fabs(cosval - cosx));
cout << cosx;
}
int main()
{
float n = 30;
cal_cos(n);
}
|
Java
import static java.lang.Math.cos;
class GFG {
static void cal_cos(float n) {
float accuracy = (float) 0.0001, x1, denominator, cosx, cosval;
n = n * (float) (3.142 / 180.0);
x1 = 1;
cosx = x1;
cosval = (float) cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
}
while (accuracy <= cosval - cosx);
System.out.println(cosx);
}
public static void main(String[] args) {
float n = 30;
cal_cos(n);
}
}
|
Python3
from math import fabs, cos
def cal_cos(n):
accuracy = 0.0001
n = n * (3.142 / 180.0)
x1 = 1
cosx = x1
cosval = cos(n)
i = 1
denominator = 2 * i * (2 * i - 1)
x1 = -x1 * n * n / denominator
cosx = cosx + x1
i = i + 1
while (accuracy <= fabs(cosval - cosx)):
denominator = 2 * i * (2 * i - 1)
x1 = -x1 * n * n / denominator
cosx = cosx + x1
i = i + 1
print('{0:.6}'.format(cosx))
if __name__ == '__main__':
n = 30
cal_cos(n)
|
C#
using System;
class GFG {
static void cal_cos(float n) {
float accuracy = (float) 0.0001, x1, denominator, cosx, cosval;
n = n * (float) (3.142 / 180.0);
x1 = 1;
cosx = x1;
cosval = (float) Math.Cos(n);
int i = 1;
do {
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
}
while (accuracy <= cosval - cosx);
Console.WriteLine(cosx);
}
static void Main() {
float n = 30;
cal_cos(n);
}
}
|
PHP
<?php
function cal_cos($n)
{
$accuracy = 0.0001;
$n = $n * (3.142 / 180.0);
$x1 = 1;
$cosx = $x1;
$cosval = cos($n);
$i = 1;
do
{
$denominator = 2 * $i * (2 * $i - 1);
$x1 = -$x1 * $n * $n / $denominator;
$cosx = $cosx + $x1;
$i = $i + 1;
} while ($accuracy <= abs($cosval - $cosx));
echo round($cosx, 6);
}
$n = 30;
cal_cos($n);
?>
|
Javascript
<script>
function cal_cos(n)
{
let accuracy = 0.0001, x1, denominator, cosx, cosval;
n = n * (3.142 / 180.0);
x1 = 1;
cosx = x1;
cosval = Math.cos(n);
let i = 1;
do
{
denominator = 2 * i * (2 * i - 1);
x1 = -x1 * n * n / denominator;
cosx = cosx + x1;
i = i + 1;
} while (accuracy <= Math.abs(cosval - cosx));
document.write(cosx.toFixed(5));
}
let n = 30;
cal_cos(n);
</script>
|
Output:
0.86602
Time Complexity: O(n)
Space Complexity: O(1)
If you like GeeksforGeeks(We know you do!) and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org.
Share your thoughts in the comments
Please Login to comment...