Probability and Statistics | Simpson’s Paradox (UC Berkeley’s Lawsuit)
Last Updated :
24 May, 2019
Simpson’s Paradox in layman’s term is the reversal of relationship within data with respect to the subgroups of data after combining those subgroups data.
For Example, If there are two departments in a university and both of them have a high probability of a woman getting accepted then after combining their data by intuition overall woman’s acceptance probability should be high but this may not be true.
Mathematically
Given, a1/b1 < c1/d1 and a2/b2 < c2/d2 then (a1+a2)/(b1+b2) < (c1+c2)/(d1+d2)?
Simpson’s Paradox says it may not be true.
7/8 < 2/2 and 1/2 < 5/8 yet,
(7+1)/(2+2) > (2+5)/(2+8)
A similar case was seen in the lawsuit against UC Berkeley’s regarding the admissions data showing that men were having a higher probability of getting applications accepted than the woman’s application. But after examining the individual departments a reverse scenario came into consideration as maximum of the departments were favoring women over men.
|
Applicants |
Admitted |
| Men |
8442 |
44% |
| Women |
4321 |
35% |
| Departments |
Men |
Women |
| Applicants |
Admitted |
Applicants |
Admitted |
| A |
825 |
62% |
108 |
82% |
| B |
560 |
63% |
25 |
68% |
| C |
325 |
37% |
593 |
34% |
| D |
417 |
33% |
375 |
35% |
| E |
191 |
28% |
393 |
24% |
| F |
272 |
6% |
341 |
7% |
Why was this happening ?
Reason:
This kind of behavior was seen because more women were applying to competitive departments with low rates of admission whereas more men were applying to less competitive departments with
high acceptance rates.
We can see from the table that 825 men have applied in comparison to 108 women in high acceptance rate department A. Whereas more girls are applying in departments with low rates like F and E. Which finally led to more men being accepted by the university than women.
Another Example:
Suppose we have a configuration as shown in figure below with two types of beans green and blue colored.
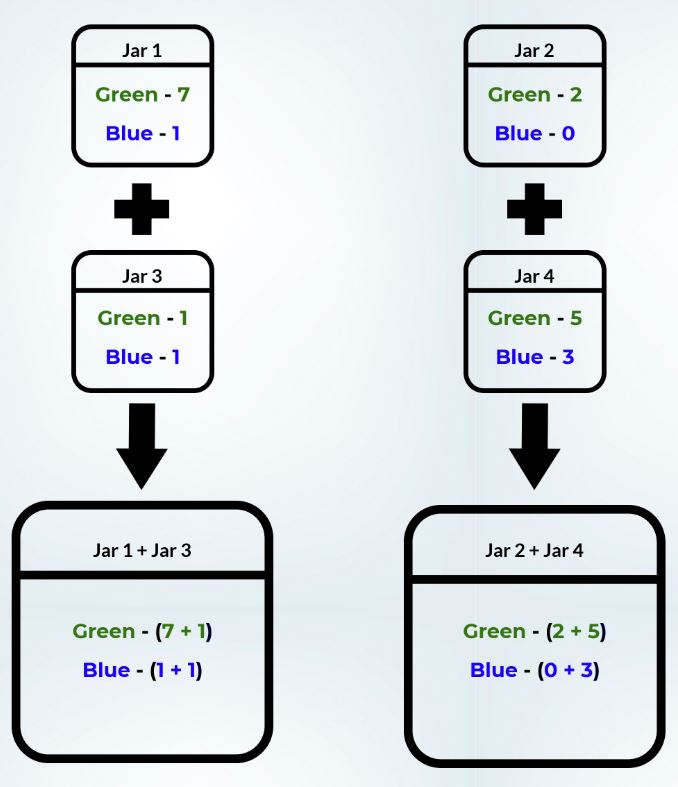
Before Mixing:
Probability of picking a green bean from Jar,
7/8 < 2/2
(Jar1) (Jar2)
1/2 < 5/8
(Jar3) (Jar4)
After Mixing:
Probability of picking a green bean from Jar
8/10 > 7/10 Inequality
(Jar1 + Jar3) (Jar2 + Jar4)
Here also we can see that initially jars 1 and 3 had a higher probability of picking green beans than Jar 2 and Jar 4 respectively, but after mixing the content of jars the relationship got reversed. After mixing, the content of Jar 2 and Jar 4 combined had a higher probability of picking green beans. This is a very simple example of Simpson’s Paradox.
Share your thoughts in the comments
Please Login to comment...