Polynomial Identities

Polynomial identity is an equation that holds for all possible values of the variables involved. It establishes a relation between two or more polynomial expressions, regardless of the specific numerical values of the variables. One common example is the polynomial identity (a+b)²=a²+ 2ab +b², which remains true for any values of a and b.

In this article, we will understand various identities of polynomials, types of polynomial identities, and their proof along with some solved examples for clear understanding.

What are Polynomial Identities?

A Polynomial Equation is a type of algebraic equation that involves multiple variables, each raised to positive integral powers. Various terms may exist within such equations with different powers of the same variable.

A Polynomial Identity, on the other hand, is an equality involving polynomial expressions that remains valid for any values assigned to its variables. Polynomial identities are particularly useful for the expansion or factorization of polynomial equations.

Polynomial identities play a significant role in algebraic manipulations, offering a versatile toolset for simplifying expressions, finding common factors, and expanding polynomial equations.

Polynomial Identity Definition

Polynomial identity is a mathematical statement asserting the equality of two polynomial expressions, holding true for all variable values.

Polynomial Identity serves as a foundational tool for simplifying and manipulating polynomial expressions in algebra, facilitating mathematical analysis and problem-solving.

Examples of Polynomial Identity

Some Examples of Polynomial Identity are:

• Square of a Binomial: (a + b)² = a² + 2ab + b²

• Difference of Squares: (a – b)(a + b) = a² – b²

• Cubing a Binomial: (a + b)³ = a³ + 3a²b + 3ab² + b³

• Sum of Cubes: a³ + b³ = (a + b)(a² – ab + b²

• Factorization of Quadratic Expression: a² – b² = (a + b)(a – b)

• Fourth Power Formula: (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

• Factorization of Quartic Expression: a⁴ – b⁴ = (a² + b²)(a² – b²) = (a² + b²)(a + b)(a – b)

• Binomial Theorem:

Types of Polynomial Identity

The types of polynomials are based on the degree or the highest power of the identities. Polynomial Identities are classified as follow:

• 2^nd Degree Polynomial Identities
• 3^rd Degree Polynomial Identities
• n Degree Polynomial Identities

2^nd Degree Polynomial Identities

Second-degree polynomial identities consists of the polynomials of degree 2 i.e. they involve the identities where maximum power of a variable in a term is 2.

Following is the list of all 2^nd Degree Polynomial Identities:

• (a+b)²=a²+b²+2ab
• (a−b)²=a²+b²−2ab
• (a+b+c)²=a²+b²+c²+2ab+2bc+2ca
• (a−b−c)²=a²−b²−c²−2ab+2bc−2ca
• (x+a)(x+b)=x²+(a+b)x+ab

3^rd Degree Polynomial Identities

Third-degree polynomial identities consists of the polynomials of degree 3 i.e. they involve the identities where maximum power of a variable in a term is 3.

Following is the list of all 3^rd Degree Polynomial Identities:

• (a+b)³=a³+b³+3ab(a+b)
• (a−b)³=a³−b³−3ab(a−b)
• a³+b³+c³–3abc=(a+b+c)(a²+b²+c²–ab–bc–ca)

n-Degree Polynomial Identities

n degree polynomial identities consists of the polynomials of degree ‘n’ i.e. they involve the identities where maximum power of a variable in a term is ‘n’. Here ‘n’ is any natural number.

Following is the formula used for all n Degree Polynomial Identities:

aⁿ-bⁿ = (a-b)[(aⁿ⁻¹)+(aⁿ⁻²)b+…+(bⁿ⁻²)a+(bⁿ⁻¹)]

where n is a natural number

• If n is even (n = 2k)
• If n is odd (n = 2k+1)

Polynomial Formulas

Following are some more polynomial formulas used in mathematics:

• a²−b²=(a+b)(a−b)
• a³−b³=(a−b)(a²+ab+b²)
• a³+b³=(a+b)(a²−ab+b²)
• a⁴−b⁴=(a²−b²)(a²+b²)
• a⁴−b⁴=(a+b)(a−b)[(a+b)²−2ab]
• 2(a²+b²)=(a+b)²+(a−b)²
• (a+b)²−(a−b)²=4ab

Proving Polynomial Identities

This segment will provide a proof of the most commonly used four polynomial identities which are:

• (a+b)² = a²+b²+2ab
• (a-b)² = a²+b²-2ab
• (a+b)(a-b)² = a²-b²
• (x + a)(x + b) = x² + x(a + b) + ab

Identity 1: (a+b)² = a²+b²+2ab

The expression (a+b)² can be expanded using the distributive property:

(a+b)² = (a+b) · (a+b)

= a · (a+b) + b · (a+b)

= a · a + a · b + b · a + b · b

= a² + ab + ba + b²

Since multiplication is commutative i.e., (ab = ba), we can simplify this expression to:

a² + 2ab + b²

∴ Proof demonstrates that (a+b)² is equal to ( a² + 2ab + b²).

Visual Proof,

Proof of (a+b)² = a² + 2ab + b² identity, let’s take a square of side a+b and divide it like the following diagram.

To prove the identity, we have to calculate the area of the square with side (a+b) which is (a+b)².

Identity 2: (a-b)² = a²+b²-2ab

To prove the polynomial identity (a – b)² = a² + b² – 2ab, we can use the distributive property and perform the necessary algebraic steps:

Starting with the left-hand side:

(a – b)² = (a – b) · (a – b)

Using the distributive property:

(a – b)² = a · (a – b) – b · (a – b)

Further simplifying:

(a – b)² = a² – ab – ab + b²

Combining like terms:

(a – b)² = a² – 2ab + b²

Now, the result matches the right-hand side of the given identity:

(a – b)² = a² + b² – 2ab

∴ Polynomial identity (a – b)² = a² + b² – 2ab is proved.

Visual Proof

Proof of (a-b)² = a²-2ab+b² identity, let’s again consider a square but this time with side “a”.

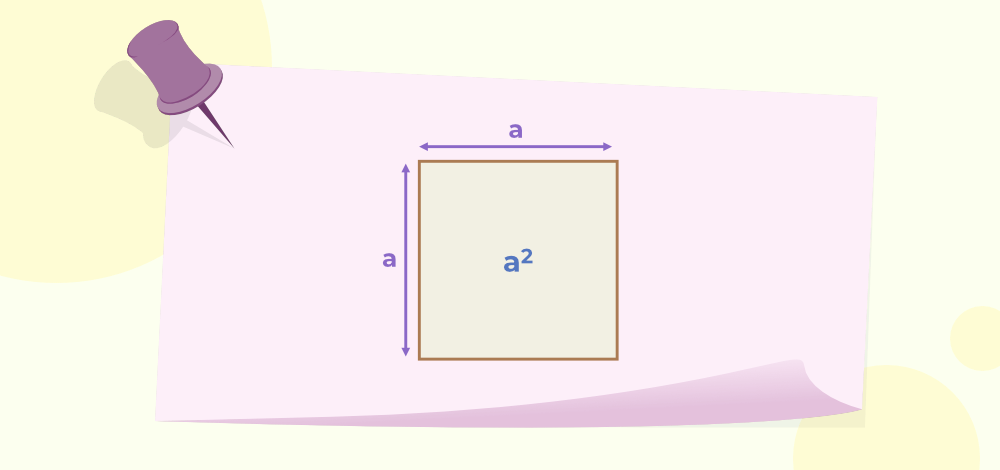
Now, take a small segment “b” from its side and divide the square as follows:

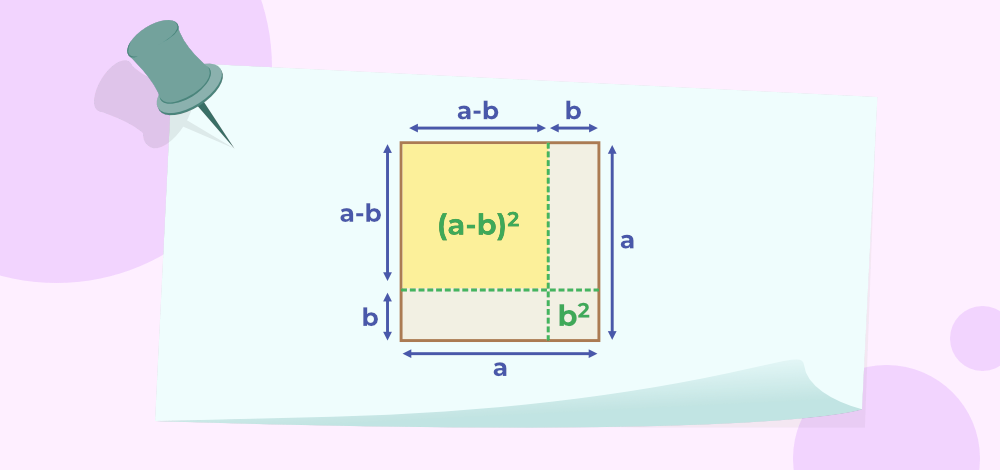
To prove the identity, we have to calculate the area of the square with side (a-b) which is (a-b)².

Identity 3: (a+b)(a-b)² = a²-b²

Use the distributive property (FOIL method) to multiply the two binomials:

(a + b)(a −b)=a (a−b) + b (a−b)

Now, multiply each term separately:

a (a −b) = a²−ab

b (a −b) = ab−b²

Combine the two results:

(a+b)(a–b)=a²−ab+ab−b²

Solving like terms:

(a+b)(a–b)=a²−b²

Hence,the polynomial identity (a+b)(a–b)=a²−b² is proved.

Identity 4: (x + a)(x + b) = x² + x(a + b) + ab

Certainly, let’s prove the polynomial identity (x + a)(x + b) = x² + x(a + b) + ab

Start with the left side of the identity: (x + a)(x + b)

Use the distributive property (FOIL method) to multiply the two binomials:

(x + a)(x + b) = x(x + b) + a(x + b)

Now, multiply each term separately:

x(x + b) = x² + xb

a(x + b) = ax + ab

Combine the two results:

(x + a)(x + b) = x² + xb + ax + a

Combine like terms:

(x + a)(x + b) = x² + x(a + b) + ab

Hence proved the polynomial identity (x + a)(x + b) = x² + x(a + b) + ab

List of Polynomial Identities

The list of some common polynomial identities which are widely used are given below:

(a + b)2	a2 + 2ab + b2
(a − b)2	a2 − 2ab + b2
(a + b)(a − b)	a2 − b2
(x + a)(x + b)	x2 + x(a + b) + ab
(a + b + c)2	a2 + b2 + c2 + 2ab + 2bc + 2ca
(a + b)3	a3 + 3a2b + 3ab2 + b3
(a − b)3	a3 − 3a2b+ 3ab2 − b3
(a)3 − (b)3	(a − b)(a2 + ab + b2)
(a)3 + (b)3	(a + b)(a2 − ab + b2)

Applications of Polynomial Identities

Applications of Polynomial identities have a wide scope in various field, but it is most commonly used in Algebraic Equation. It is used in solving Algebraic equations are mentioned below:

Use in Solving Algebraic Equations

Following are the uses of Polynomial Identities in Solving Algebraic Equations:

• Factoring Equations: Polynomial identities help factorize algebraic expressions, making it easier to solve equations.

• Root Finding: Identifying roots or solutions of equations by manipulating expressions using polynomial identities.

• Solving Quadratic Equations: Quadratic identities, derived from polynomial identities, aid in solving quadratic equations efficiently.

• Simplification of Expressions: Applying polynomial identities simplifies complex expressions, facilitating equation simplification.

• Expression Substitution: Substituting variables with expressions derived from polynomial identities to simplify equations.

• System of Equations: Polynomial identities contribute to solving systems of equations by expressing relationships between variables.

• Functional Analysis: Understanding the behavior of functions and their solutions becomes easier through the application of polynomial identities.

Some Other Applications of Polynomial Identities are:

• Mathematical Modeling: Represent and analyze real-world phenomena for predictions and conclusions.

• Computer Science: Used in algorithm design, error correction codes, and cryptography.

• Physics and Engineering: Applied for modeling physical systems, solving equations, and analyzing structures.

• Statistical Analysis: Provide tools for expressing relationships and analyzing data patterns.

• Optimization Problems: Used in solving problems to find maximum or minimum values.

• Number Theory: Contribute to the study of integers and their properties in mathematics.

Read More,

• Polynomial
• Polynomial Formula
• Algebraic Identities of a Polynomial

Solved Examples on Polynomial Identities

Example 1: Calculate the product of (x – 2)²

Solution:

Expanding this expression involves multiplying each term in the bracket by itself:

(x – 2)² = (x – 2)(x – 2)

Using the distributive property:

= x(x) – x(2) – 2(x) + 2(2)

Simplifying further:

= x² – 2x – 2x + 4

Combining like terms:

= x² – 4x + 4

So, (x – 2)² expands to (x² – 4x + 4).

Example 2: Evaluate (4a + 7b)²

Solution:

Given (4a + 7b)²

Using the formula (a + b)² = (a² + 2ab + b²), we can apply it to our expression:

(4a + 7b)² = (4a)² + 2(4a)(7b) + (7b)²

Simplifying further:

16a² + 56ab + 49b²

So, (4a + 7b)² simplifies to (16a² + 56ab + 49b²)

Example 3: Simplify (2m + 3n)² – (m – 2n)²

Solution:

We know (a+b)² = a²+b²+2ab

Apply the above identity in (2m + 3n)² and (m – 2n)²

(2m + 3n)² = 4m² + 12mn + 9n²

similarly,

(m – 2n)² = m² – 4mn + 4n²

Now, subtracting the second expression from the first:

(4m² + 12mn + 9n²) – (m² – 4mn + 4n²)

Combine like terms:

4m² – m²+ 12mn + 4mn + 9n² – 4n²

Solving the above equation we get:

3m² + 16mn + 5n²

Hence, (2m + 3n)² – (m – 2n)² simplifies to (3m² + 16mn + 5n²)

Polynomial Identity Practice Questions

Q1. Expand and simplify: (x + 3)²

Q2. Find the product: (a – b)²

Q3. Determine the value of: (2x + 5)²

Q4. Simplify: (m + n)²– (m – n)²

Q5. Expand and simplify: (3p – 4q)²

Polynomial Identity: FAQs

What is a Polynomial?

A polynomial is a mathematical expression of variables, coefficients, and exponents combined using addition, subtraction, multiplication, and non-negative integer exponents.

What is Polynomial Identity?

A polynomial identity is a mathematical expression that remains true for all values of the variables involved. These identities are fundamental in algebra, representing equality between two polynomial expressions regardless of specific numerical values.

What are Identities of Algebra?

In algebra, identities are equations that hold true for all possible values of the variables. These include polynomial identities and other fundamental equations that serve as the basis for various mathematical manipulations.

What are 3rd Degree Polynomial Identities?

The 3rd degree polynomial identities are:

• (a+b)³ = a³+b³+3ab(a+b)
• (a−b)³ = a³−b³−3ab(a−b)
• a³+b³+c³–3abc = (a+b+c)(a²+b²+c²–ab–bc–ca)

How to Prove a Polynomial Identity? 

Proving a polynomial identity involves demonstrating that both sides of the equation are equivalent by performing algebraic manipulations, applying known identities, and ensuring the equality holds for all values of the variables.

What are Eight Common Polynomial Identities? 

Eight common polynomial identities include:

• (a+b)² = a²+b²+2ab
• (a-b)² = a²+b²-2ab
• (a+b)(a-b) = a²-b²
• (x+a)(x+b) = x²+x(a+b)+ab
• (a+b)³ = a³+3a²b+3ab²+b³
• (a-b)³ = a³-3a²b+3ab²-b³
• (a+b+c)² = a²+b²+c²+2ab+2bc+2ca
• a³+b³+c³–3abc=(a+b+c)(a²+b²+c²–ab–bc–ca)

Can Polynomial Identities be Applied to Complex Numbers?

Yes, polynomial identities can be applied to complex numbers. The rules of algebra, including polynomial identities, extend to complex numbers, allowing for manipulation and solution in the complex number domain.

What is Importance of Polynomial Identities in Algebra? 

Polynomial identities play a crucial role in algebra by providing tools for simplifying expressions, solving equations, and understanding the relationships between variables.

Difference Between Identity and Polynomial?

An identity is a mathematical equation that holds true for all values of the variables, while a polynomial is an algebraic expression consisting of variables, coefficients, and exponents, often representing a sum of terms.

What is Polynomial Formula?

A polynomial formula is a general expression representing a polynomial with variables, coefficients, and exponents. It follows the form P(x) = a_nxⁿ + a_(n-1)x^(n-1) + … + a₁x + a₀, where P(x) is the polynomial, a_n to a₀ are coefficients, and n is the degree.

What is Coefficient of xy in (x + y)²?

Expanding (x + y)² gives x² + 2xy + y². The coefficient of xy is 2, as it appears in the term 2xy.

What is Identity of Quadratic Polynomial?

A common quadratic polynomial identity is (a + b)² = a² + 2ab + b², where ‘a’ and ‘b’ are variables