Number of ways to color N-K blocks using given operation
Last Updated :
12 Oct, 2022
Given N blocks, out of which K is colored. These K-colored blocks are denoted by an array arr[]. The task is to count the number of ways to color the remaining uncolored blocks such that only any one of the adjacent blocks, of a colored block, can be colored in one step. Print the answer with modulo 109+7.
Examples:
Input: N = 6, K = 3, arr[] = {1, 2, 6}
Output: 4
Explanation:
The following are the 4 ways to color the blocks(each set represents the order in which blocks are colored):
1. {3, 4, 5}
2. {3, 5, 4}
3. {5, 3, 4}
4. {5, 4, 3}
Input: N = 9, K = 3, A = [3, 6, 7]
Output: 180
Naive Approach: The idea is to use recursion. Below are the steps:
- Traverse each block from 1 to N.
- If the current block(say b) is not colored, then check whether one of the adjacent blocks is colored or not.
- If the adjacent block is colored, then color the current block and recursively iterate to find the next uncolored block.
- After the above recursive call ends, then, uncolored the block for the blockquotevious recursive call and repeat the above steps for the next uncolored block.
- The count of coloring the blocks in all the above recursive calls gives the number of ways to color the uncolored block.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
int countWays(int colored[], int count,
int n)
{
if (count == n) {
return 1;
}
int answer = 0;
for (int i = 1; i < n + 1; i++) {
if (colored[i] == 0) {
if (colored[i - 1] == 1
|| colored[i + 1] == 1) {
colored[i] = 1;
answer = (answer
+ countWays(colored,
count + 1,
n))
% mod;
colored[i] = 0;
}
}
}
return answer;
}
int waysToColor(int arr[], int n, int k)
{
int colored[n + 2] = { 0 };
for (int i = 0; i < k; i++) {
colored[arr[i]] = 1;
}
return countWays(colored, k, n);
}
int main()
{
int N = 6;
int K = 3;
int arr[K] = { 1, 2, 6 };
cout << waysToColor(arr, N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int mod = 1000000007;
static int countWays(int colored[],
int count, int n)
{
if (count == n)
{
return 1;
}
int answer = 0;
for (int i = 1; i < n + 1; i++)
{
if (colored[i] == 0)
{
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
colored[i] = 1;
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
colored[i] = 0;
}
}
}
return answer;
}
static int waysToColor(int arr[],
int n, int k)
{
int colored[] = new int[n + 2];
for (int i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
return countWays(colored, k, n);
}
public static void main(String[] args)
{
int N = 6;
int K = 3;
int arr[] = { 1, 2, 6 };
System.out.print(waysToColor(arr, N, K));
}
}
|
Python3
mod = 1000000007
def countWays(colored, count, n):
if (count == n):
return 1
answer = 0
for i in range(1, n + 1):
if (colored[i] == 0):
if (colored[i - 1] == 1 or
colored[i + 1] == 1):
colored[i] = 1
answer = ((answer +
countWays(colored,
count + 1,
n)) % mod)
colored[i] = 0
return answer
def waysToColor( arr, n, k):
colored = [0] * (n + 2)
for i in range(k):
colored[arr[i]] = 1
return countWays(colored, k, n)
if __name__ == "__main__":
N = 6
K = 3
arr = [ 1, 2, 6 ]
print(waysToColor(arr, N, K))
|
C#
using System;
class GFG{
static int mod = 1000000007;
static int countWays(int []colored,
int count, int n)
{
if (count == n)
{
return 1;
}
int answer = 0;
for (int i = 1; i < n + 1; i++)
{
if (colored[i] == 0)
{
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
colored[i] = 1;
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
colored[i] = 0;
}
}
}
return answer;
}
static int waysToColor(int []arr,
int n, int k)
{
int []colored = new int[n + 2];
for (int i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
return countWays(colored, k, n);
}
public static void Main()
{
int N = 6;
int K = 3;
int []arr = { 1, 2, 6 };
Console.Write(waysToColor(arr, N, K));
}
}
|
Javascript
<script>
let mod = 1000000007;
function countWays(colored,
count, n)
{
if (count == n)
{
return 1;
}
let answer = 0;
for (let i = 1; i < n + 1; i++)
{
if (colored[i] == 0)
{
if (colored[i - 1] == 1 ||
colored[i + 1] == 1)
{
colored[i] = 1;
answer = (answer +
countWays(colored,
count + 1,
n)) % mod;
colored[i] = 0;
}
}
}
return answer;
}
function waysToColor(arr, n, k)
{
let colored = Array.from({length: n+2}, (_, i) => 0);
for (let i = 0; i < k; i++)
{
colored[arr[i]] = 1;
}
return countWays(colored, k, n);
}
let N = 6;
let K = 3;
let arr = [ 1, 2, 6 ];
document.write(waysToColor(arr, N, K));
</script>
|
Time Complexity: O(NN-K)
Auxiliary Space: O(N)
Efficient Approach: For solving this problem efficiently we will use the concept of Permutation and Combination. Below are the steps:
1. If the number of blocks between two consecutive colored blocks is x, then the number of ways to color these set of blocks is given by:
ways = 2x-1
2. Coloring each set of uncolored blocks is independent of the other. Suppose there are x blocks in one section and y blocks in the other section. To find the total combination when the two sections are merged is given by:
total combinations = 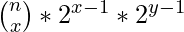
3. Sort the colored block indices to find the length of each uncolored block section and iterate and find the combination of each two-section using the above formula.
4. Find the Binomial Coefficient using the approach discussed in this article.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
int waysToColor(int arr[], int n, int k)
{
int powOf2[500] = { 0 };
int c[500][500];
for (int i = 0; i <= n; i++) {
c[i][0] = 1;
for (int j = 1; j <= i; j++) {
c[i][j] = (c[i - 1][j]
+ c[i - 1][j - 1])
% mod;
}
}
powOf2[0] = powOf2[1] = 1;
for (int i = 2; i <= n; i++) {
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
sort(arr, arr + k);
int answer = 1;
for (int i = 0; i < k; i++) {
int x = arr[i] - (i - 1 >= 0
? arr[i - 1]
: 0)
- 1;
answer *= c[rem][x] % mod * (i != 0
&& i != k - 1
? powOf2[x]
: 1)
% mod;
rem -= x;
}
return answer;
}
int main()
{
int N = 6;
int K = 3;
int arr[K] = { 1, 2, 6 };
cout << waysToColor(arr, N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int mod = 1000000007;
static int waysToColor(int arr[], int n, int k)
{
int powOf2[] = new int[500];
int [][]c = new int[500][500];
for(int i = 0; i <= n; i++)
{
c[i][0] = 1;
for(int j = 1; j <= i; j++)
{
c[i][j] = (c[i - 1][j] +
c[i - 1][j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
for(int i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
Arrays.sort(arr);
int answer = 1;
for(int i = 0; i < k; i++)
{
int x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
answer *= c[rem][x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
return answer;
}
public static void main(String[] args)
{
int N = 6;
int K = 3;
int arr[] = { 1, 2, 6 ,0 };
System.out.print(waysToColor(arr, N, K));
}
}
|
Python3
mod = 1000000007
def waysToColor(arr, n, k):
global mod
powOf2 = [0 for i in range(500)]
c = [[0 for i in range(500)] for j in range(500)]
for i in range(n + 1):
c[i][0] = 1;
for j in range(1, i + 1):
c[i][j] = (c[i - 1][j]+ c[i - 1][j - 1])% mod;
powOf2[0] = 1
powOf2[1] = 1;
for i in range(2, n + 1):
powOf2[i] = (powOf2[i - 1] * 2) % mod;
rem = n - k;
arr[k] = n + 1;
k += 1
arr.sort()
answer = 1;
for i in range(k):
x = 0
if i - 1 >= 0:
x = arr[i] - arr[i - 1] -1
else:
x = arr[i] - 1
answer = answer * (c[rem][x] % mod) * ((powOf2[x] if (i != 0 and i != k - 1) else 1))% mod
rem -= x;
return answer;
if __name__=='__main__':
N = 6;
K = 3;
arr = [ 1, 2, 6, 0]
print(waysToColor(arr, N, K))
|
C#
using System;
class GFG{
static int mod = 1000000007;
static int waysToColor(int []arr, int n, int k)
{
int []powOf2 = new int[500];
int [,]c = new int[500, 500];
for(int i = 0; i <= n; i++)
{
c[i, 0] = 1;
for(int j = 1; j <= i; j++)
{
c[i, j] = (c[i - 1, j] +
c[i - 1, j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
for(int i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
int rem = n - k;
arr[k++] = n + 1;
Array.Sort(arr);
int answer = 1;
for(int i = 0; i < k; i++)
{
int x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
answer *= c[rem, x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
return answer;
}
public static void Main(String[] args)
{
int N = 6;
int K = 3;
int []arr = { 1, 2, 6, 0 };
Console.Write(waysToColor(arr, N, K));
}
}
|
Javascript
<script>
let mod = 1000000007;
function waysToColor(arr,n,k)
{
let powOf2 = new Array(500);
let c = new Array(500);
for(let i=0;i<500;i++)
{
c[i]=new Array(500);
for(let j=0;j<500;j++)
{
c[i][j]=0;
}
}
for(let i = 0; i <= n; i++)
{
c[i][0] = 1;
for(let j = 1; j <= i; j++)
{
c[i][j] = (c[i - 1][j] +
c[i - 1][j - 1]) % mod;
}
}
powOf2[0] = powOf2[1] = 1;
for(let i = 2; i <= n; i++)
{
powOf2[i] = powOf2[i - 1] * 2 % mod;
}
let rem = n - k;
arr[k++] = n + 1;
arr.sort(function(a,b){return a-b;});
let answer = 1;
for(let i = 0; i < k; i++)
{
let x = arr[i] - (i - 1 >= 0 ?
arr[i - 1] : 0) - 1;
answer *= c[rem][x] % mod * (i != 0 &&
i != k - 1 ?
powOf2[x] : 1) %
mod;
rem -= x;
}
return answer;
}
let N = 6;
let K = 3;
let arr=[ 1, 2, 6 ,0];
document.write(waysToColor(arr, N, K));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(52 * 104)
Share your thoughts in the comments
Please Login to comment...