Minimum number of blocks required to form Hollow Rectangular Prism
Last Updated :
01 Nov, 2023
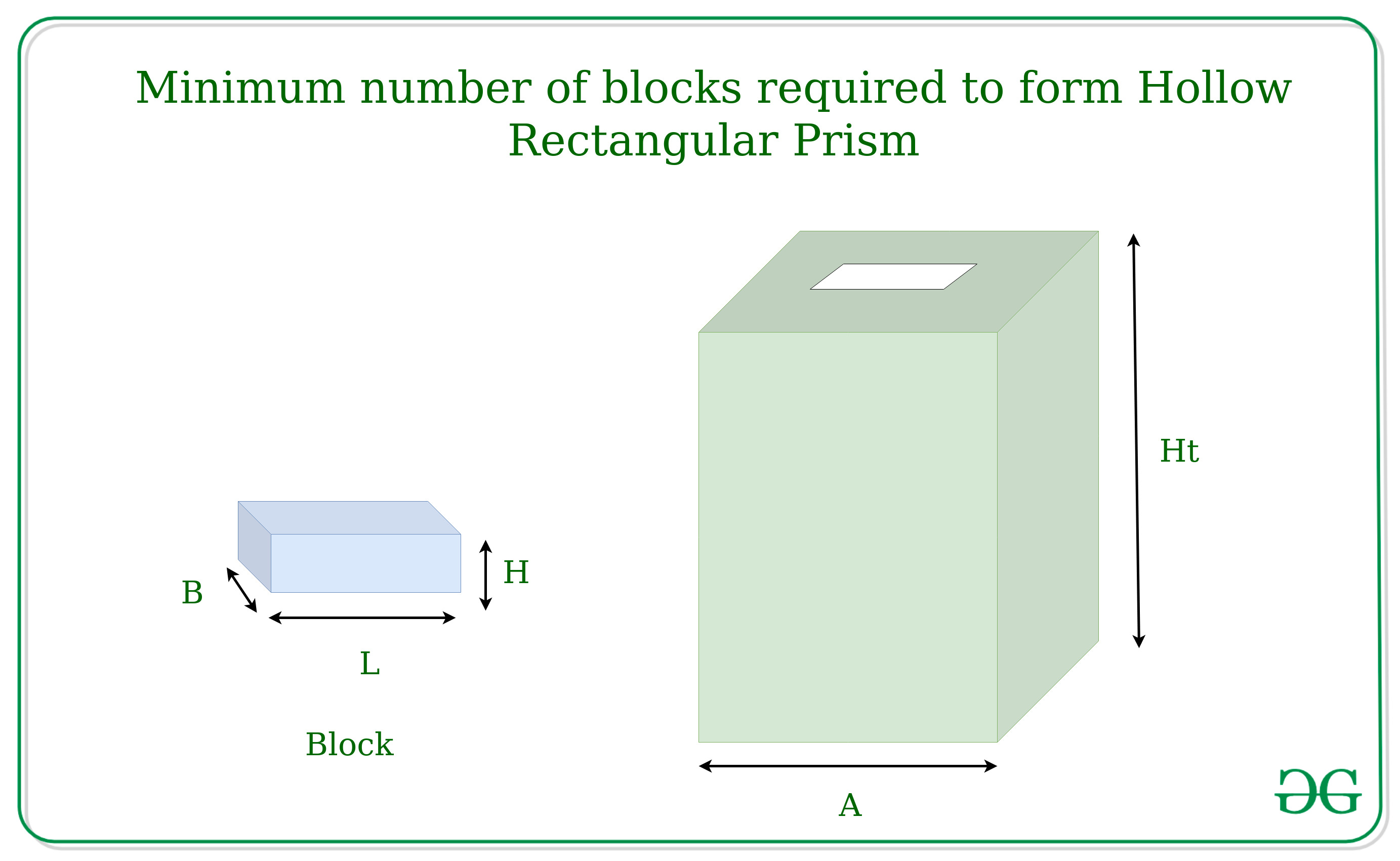
Given the dimensions of a block L, B and H, the task is to form a Hollow Rectangular prism of length A and height Ht such that minimum no of blocks are required.
Examples:
Input: L = 40, B = 30, H = 10 & A = 500, Ht = 300
Output: 500
Input: L = 30, B = 20, H = 20, & A = 600, Ht =240
Output: 960
Approach:
Calculate the minimum number of blocks required in each layer which can be done by setting the blocks in such a way that it occupies maximum length by finding the number of blocks required for the 4 sides of the rectangular prism, then choose for the block side which can be taken as the height of the block. From width or the height whichever is greater is taken as height.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void disp(int row_no, int block)
{
cout << row_no * block;
}
int row(int ht, int h)
{
return ht / h;
}
void calculate(int l, int w, int h, int a, int ht)
{
int no_block = (4 * a) / l;
int row_no;
if (h < w)
row_no = row(ht, w);
else
row_no = row(ht, h);
disp(row_no, no_block);
}
int main()
{
int l = 50, w = 20, h = 35;
int a = 700;
int ht = 140;
calculate(l, w, h, a, ht);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void disp(int row_no, int block)
{
System.out.print(row_no * block);
}
static int row(int ht, int h)
{
return ht / h;
}
static void calculate(int l, int w, int h, int a, int ht)
{
int no_block = (4 * a) / l;
int row_no;
if (h < w)
row_no = row(ht, w);
else
row_no = row(ht, h);
disp(row_no, no_block);
}
public static void main(String[] args)
{
int l = 50, w = 20, h = 35;
int a = 700;
int ht = 140;
calculate(l, w, h, a, ht);
}
}
|
Python 3
def disp(row_no,block):
print(row_no * block)
def row(ht, h):
return ht // h
def calculate(l, w, h, a, ht):
no_block = (4 * a) // l
if (h < w):
row_no = row(ht, w)
else:
row_no = row(ht, h)
disp(row_no, no_block)
if __name__ == '__main__':
l = 50
w = 20
h = 35
a = 700
ht = 140
calculate(l, w, h, a, ht)
|
C#
using System;
class GFG{
static void disp(int row_no, int block)
{
Console.Write(row_no * block);
}
static int row(int ht, int h)
{
return ht / h;
}
static void calculate(int l, int w, int h,
int a, int ht)
{
int no_block = (4 * a) / l;
int row_no;
if (h < w)
row_no = row(ht, w);
else
row_no = row(ht, h);
disp(row_no, no_block);
}
public static void Main(String[] args)
{
int l = 50, w = 20, h = 35;
int a = 700;
int ht = 140;
calculate(l, w, h, a, ht);
}
}
|
Javascript
<script>
function disp( row_no, block)
{
document.write( row_no * block);
}
function row( ht, h)
{
return ht / h;
}
function calculate( l, w, h, a, ht)
{
let no_block = (4 * a) / l;
let row_no;
if (h < w)
row_no = row(ht, w);
else
row_no = row(ht, h);
disp(row_no, no_block);
}
let l = 50, w = 20, h = 35;
let a = 700;
let ht = 140;
calculate(l, w, h, a, ht);
</script>
|
Time complexity: O(1) as doing constant operations
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...