Number of values of b such that a = b + (a^b)
Last Updated :
20 Aug, 2022
Given an integer 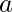 . Find the number of solutions of
. Find the number of solutions of 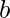 which satisfies the equation:
which satisfies the equation:
a = b + (a^b)
Examples:
Input: a = 4
Output: 2
The only values of b are 0 and 4 itself.
Input: a = 3
Output: 4
A naive solution is to iterate from 0 to 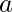 and count the number of values that satisfies the given equation. We need to traverse only till
and count the number of values that satisfies the given equation. We need to traverse only till 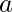 since any value greater than
since any value greater than 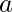 will give the XOR value >
will give the XOR value > 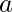 , hence cannot satisfy the equation.
, hence cannot satisfy the equation.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSolutions(int a)
{
int count = 0;
for (int i = 0; i <= a; i++) {
if (a == (i + (a ^ i)))
count++;
}
return count;
}
int main()
{
int a = 3;
cout << countSolutions(a);
}
|
Java
import java.io.*;
class GFG {
static int countSolutions(int a)
{
int count = 0;
for (int i = 0; i <= a; i++) {
if (a == (i + (a ^ i)))
count++;
}
return count;
}
public static void main (String[] args) {
int a = 3;
System.out.println( countSolutions(a));
}
}
|
Python3
def countSolutions(a):
count = 0
for i in range(a + 1):
if (a == (i + (a ^ i))):
count += 1
return count
if __name__ == "__main__":
a = 3
print(countSolutions(a))
|
C#
using System;
class GFG
{
static int countSolutions(int a)
{
int count = 0;
for (int i = 0; i <= a; i++)
{
if (a == (i + (a ^ i)))
count++;
}
return count;
}
public static void Main ()
{
int a = 3;
Console.WriteLine(countSolutions(a));
}
}
|
PHP
<?php
function countSolutions($a)
{
$count = 0;
for ($i = 0; $i <= $a; $i++)
{
if ($a == ($i + ($a ^ $i)))
$count++;
}
return $count;
}
$a = 3;
echo countSolutions($a);
?>
|
Javascript
<script>
function countSolutions(a)
{
let count = 0;
for (let i = 0; i <= a; i++) {
if (a == (i + (a ^ i)))
count++;
}
return count;
}
let a = 3;
document.write(countSolutions(a));
</script>
|
Time Complexity: O(a), since there runs a loop for a times.
Auxiliary Space: O(1), since no extra space has been taken.
An Efficient Approach is to observe a pattern of answers when we write the possible solutions for different values of 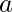 . Only the set bits are used to determine the number of possible answers. The answer to the problem will always be 2^(number of set bits) which can be determined by observation.
. Only the set bits are used to determine the number of possible answers. The answer to the problem will always be 2^(number of set bits) which can be determined by observation.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSolutions(int a)
{
int count = __builtin_popcount(a);
count = pow(2, count);
return count;
}
int main()
{
int a = 3;
cout << countSolutions(a);
}
|
Java
import java.io.*;
class GFG
{
static int countSolutions(int a)
{
int count = Integer.bitCount(a);
count =(int) Math.pow(2, count);
return count;
}
public static void main (String[] args)
{
int a = 3;
System.out.println(countSolutions(a));
}
}
|
Python3
def countSolutions(a):
count = bin(a).count('1')
return 2 ** count
if __name__ == "__main__":
a = 3
print(countSolutions(a))
|
C#
class GFG
{
static int countSolutions(int a)
{
int count = bitCount(a);
count =(int) System.Math.Pow(2, count);
return count;
}
static int bitCount(int n)
{
int count = 0;
while (n != 0)
{
count++;
n &= (n - 1);
}
return count;
}
public static void Main()
{
int a = 3;
System.Console.WriteLine(countSolutions(a));
}
}
|
PHP
<?php
function countSolutions($a)
{
$count = bitCount($a);
$count = (int)pow(2, $count);
return $count;
}
function bitCount($n)
{
$count = 0;
while ($n != 0)
{
$count++;
$n &= ($n - 1);
}
return $count;
}
$a = 3;
echo (countSolutions($a));
?>
|
Javascript
<script>
function bitCount(n)
{
let count = 0;
while (n != 0)
{
count++;
n &= (n - 1);
}
return count;
}
function countSolutions(a)
{
let count = bitCount(a);
count = Math.pow(2, count);
return count;
}
let a = 3;
document.write(countSolutions(a));
</script>
|
Time Complexity: O(log N) since inbuilt pow function has been used which takes logarithmic time.
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...