Booth algorithm gives a procedure for multiplying binary integers in signed 2’s complement representation in efficient way, i.e., less number of additions/subtractions required. It operates on the fact that strings of 0’s in the multiplier require no addition but just shifting and a string of 1’s in the multiplier from bit weight 2^k to weight 2^m can be treated as 2^(k+1 ) to 2^m. As in all multiplication schemes, booth algorithm requires examination of the multiplier bits and shifting of the partial product. Prior to the shifting, the multiplicand may be added to the partial product, subtracted from the partial product, or left unchanged according to following rules:
- The multiplicand is subtracted from the partial product upon encountering the first least significant 1 in a string of 1’s in the multiplier
- The multiplicand is added to the partial product upon encountering the first 0 (provided that there was a previous ‘1’) in a string of 0’s in the multiplier.
- The partial product does not change when the multiplier bit is identical to the previous multiplier bit.
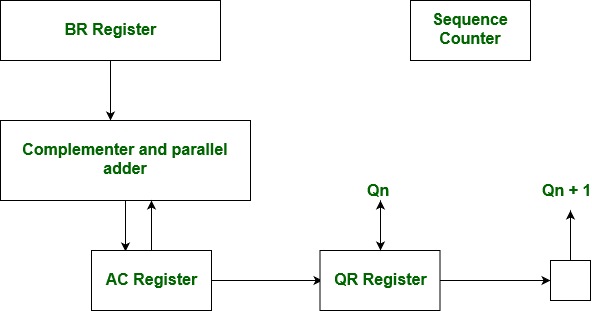
Hardware Implementation of Booths Algorithm – The hardware implementation of the booth algorithm requires the register configuration shown in the figure below.
Booth’s Algorithm Flowchart –
We name the register as A, B and Q, AC, BR and QR respectively. Qn designates the least significant bit of multiplier in the register QR. An extra flip-flop Qn+1is appended to QR to facilitate a double inspection of the multiplier.The flowchart for the booth algorithm is shown below.

Flow chart of Booth’s Algorithm.
AC and the appended bit Qn+1 are initially cleared to 0 and the sequence SC is set to a number n equal to the number of bits in the multiplier. The two bits of the multiplier in Qn and Qn+1are inspected. If the two bits are equal to 10, it means that the first 1 in a string has been encountered. This requires subtraction of the multiplicand from the partial product in AC. If the 2 bits are equal to 01, it means that the first 0 in a string of 0’s has been encountered. This requires the addition of the multiplicand to the partial product in AC. When the two bits are equal, the partial product does not change. An overflow cannot occur because the addition and subtraction of the multiplicand follow each other. As a consequence, the 2 numbers that are added always have a opposite signs, a condition that excludes an overflow. The next step is to shift right the partial product and the multiplier (including Qn+1). This is an arithmetic shift right (ashr) operation which AC and QR to the right and leaves the sign bit in AC unchanged. The sequence counter is decremented and the computational loop is repeated n times. Product of negative numbers is important, while multiplying negative numbers we need to find 2’s complement of the number to change its sign, because it’s easier to add instead of performing binary subtraction. product of two negative number is demonstrated below along with 2’s complement.
Example – A numerical example of booth’s algorithm is shown below for n = 4. It shows the step by step multiplication of -5 and -7.
BR = -5 = 1011,
BR' = 0100, <-- 1's Complement (change the values 0 to 1 and 1 to 0)
BR'+1 = 0101 <-- 2's Complement (add 1 to the Binary value obtained after 1's complement)
QR = -7 = 1001 <-- 2's Complement of 0111 (7 = 0111 in Binary)
The explanation of first step is as follows: Qn+1
AC = 0000, QR = 1001, Qn+1 = 0, SC = 4
Qn Qn+1 = 10
So, we do AC + (BR)'+1, which gives AC = 0101
On right shifting AC and QR, we get
AC = 0010, QR = 1100 and Qn+1 = 1
Product is calculated as follows:
Product = AC QR
Product = 0010 0011 = 35
Advantages:
Faster than traditional multiplication: Booth’s algorithm is faster than traditional multiplication methods, requiring fewer steps to produce the same result.
Efficient for signed numbers: The algorithm is designed specifically for multiplying signed binary numbers, making it a more efficient method for multiplication of signed numbers than traditional methods.
Lower hardware requirement: The algorithm requires fewer hardware resources than traditional multiplication methods, making it more suitable for applications with limited hardware resources.
Widely used in hardware: Booth’s algorithm is widely used in hardware implementations of multiplication operations, including digital signal processors, microprocessors, and FPGAs.
Disadvantages:
Complex to understand: The algorithm is more complex to understand and implement than traditional multiplication methods.
Limited applicability: The algorithm is only applicable for multiplication of signed binary numbers, and cannot be used for multiplication of unsigned numbers or numbers in other formats without additional modifications.
Higher latency: The algorithm requires multiple iterations to calculate the result of a single multiplication operation, which increases the latency or delay in the calculation of the result.
Higher power consumption: The algorithm consumes more power compared to traditional multiplication methods, especially for larger inputs.
Application of Booth’s Algorithm:
1. Chip and computer processors: Corner’s Calculation is utilized in the equipment execution of number-crunching rationale units (ALUs) inside microchips and computer chips. These parts are liable for performing number juggling and coherent procedure on twofold information. Proficient duplication is fundamental in different applications, including logical registering, designs handling, and cryptography. Corner’s Calculation lessens the quantity of piece movements and augmentations expected to perform duplication, bringing about quicker execution and better in general execution.
2. Digital Signal Processing (DSP): DSP applications frequently include complex numerical tasks, for example, sifting and convolution. Duplicating enormous twofold numbers is a principal activity in these errands. Corner’s Calculation permits DSP frameworks to perform duplications all the more productively, empowering ongoing handling of sound, video, and different sorts of signs.
3. Hardware Accelerators: Many particular equipment gas pedals are intended to perform explicit assignments more productively than broadly useful processors. Corner’s Calculation can be integrated into these gas pedals to accelerate augmentation activities in applications like picture handling, brain organizations, and AI.
4. Cryptography: Cryptographic calculations, like those utilized in encryption and computerized marks, frequently include particular exponentiation, which requires proficient duplication of huge numbers. Corner’s Calculation can be utilized to speed up the measured augmentation step in these calculations, working on the general proficiency of cryptographic tasks.
5. High-Performance Computing (HPC): In logical reenactments and mathematical calculations, enormous scope augmentations are oftentimes experienced. Corner’s Calculation can be carried out in equipment or programming to advance these duplication tasks and improve the general exhibition of HPC frameworks.
6. Implanted Frameworks: Inserted frameworks frequently have restricted assets regarding handling power and memory. By utilizing Corner’s Calculation, fashioners can upgrade augmentation activities in these frameworks, permitting them to perform all the more proficiently while consuming less energy.
7. Network Parcel Handling: Organization gadgets and switches frequently need to perform estimations on bundle headers and payloads. Augmentation activities are regularly utilized in these estimations, and Corner’s Calculation can assist with diminishing handling investment utilization in these gadgets.
8. Advanced Channels and Balancers: Computerized channels and adjusters in applications like sound handling and correspondence frameworks require productive augmentation of coefficients with input tests. Stall’s Calculation can be utilized to speed up these increases, prompting quicker and more precise sifting activities.
Basically, Corner’s Calculation finds its application any place productive paired duplication is required, particularly in situations where speed, power proficiency, and equipment streamlining are significant elements.
Best Case and Worst Case Occurrence: Best case is when there is a large block of consecutive 1’s and 0’s in the multipliers, so that there is minimum number of logical operations taking place, as in addition and subtraction. Worst case is when there are pairs of alternate 0’s and 1’s, either 01 or 10 in the multipliers, so that maximum number of additions and subtractions are required. GATE Practice Questions –
- GATE IT 2008 | Question 40
- GATE IT 2006 | Question 38
- GATE IT 2005 | Question 8
- GATE CS 1996 | Question 23
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...