Minimum cost required to connect all houses in a city

Given a 2D array houses[][] consisting of N 2D coordinates {x, y} where each coordinate represents the location of each house, the task is to find the minimum cost to connect all the houses of the city.

Cost of connecting two houses is the Manhattan Distance between the two points (x_i, y_i) and (x_j, y_j) i.e., |x_i – x_j| + |y_i – y_j|, where |p| denotes the absolute value of p.

Examples:

Input: houses[][] = [[0, 0], [2, 2], [3, 10], [5, 2], [7, 0]]
Output: 20
Explanation:

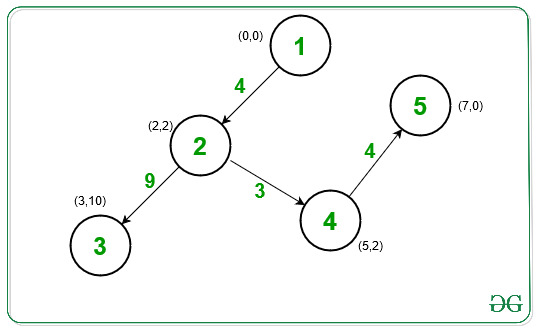
Connect house 1 (0, 0) with house 2 (2, 2) with cost = 4
Connect house 2 (2, 2) with house 3 (3, 10) with cost =9 
Connect house 2 (2, 2) with house 4 (5, 2) with cost =3 
At last, connect house 4 (5, 2) with house 5 (7, 0) with cost 4.
All the houses are connected now.
The overall minimum cost is 4 + 9 + 3 + 4 = 20.

Input: houses[][] = [[3, 12], [-2, 5], [-4, 1]]
Output: 18
Explanation:
Connect house 1 (3, 12) with house 2 (-2, 5) with cost = 12
Connect house 2 (-2, 5) with house 3 (-4, 1) with cost = 6
All the houses are connected now.
The overall minimum cost is 12 + 6 = 18.

Approach: The idea is to create a weighted graph from the given information with weights between any pair of edges equal to the cost of connecting them, say C_i i.e., the Manhattan distance between the two coordinates. Once the graph is generated, apply Kruskal’s Algorithm to find the Minimum Spanning Tree of the graph using Disjoint Set. Finally, print the minimum cost.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

vector<int> parent, size;

// Utility function to find set of an
// element v using path compression
// technique
int find_set(int v)
{
    // If v is the parent
    if (v == parent[v])
        return v;

    // Otherwise, recursively
    // find its parent
    return parent[v]
           = find_set(parent[v]);
}

// Function to perform union
// of the sets a and b
int union_sets(int a, int b)
{
    // Find parent of a and b
    a = find_set(a);
    b = find_set(b);

    // If parent are different
    if (a != b) {

        // Swap Operation
        if (size[a] < size[b])
            swap(a, b);

        // Update parent of b as a
        parent[b] = a;
        size[a] += size[b];
        return 1;
    }

    // Otherwise, return 0
    return 0;
}

// Function to create a Minimum Cost
// Spanning tree for given houses
void MST(int houses[][2], int n)
{
    // Stores adjacency list of graph
    vector<pair<int, pair<int, int> > > v;

    // Traverse each coordinate
    for (int i = 0; i < n; i++) {

        for (int j = i + 1; j < n; j++) {

            // Find the Manhattan distance
            int p = abs(houses[i][0]
                        - houses[j][0]);

            p += abs(houses[i][1]
                     - houses[j][1]);

            // Add the edges
            v.push_back({ p, { i, j } });
        }
    }

    parent.resize(n);
    size.resize(n);

    // Sort all the edges
    sort(v.begin(), v.end());

    // Initialize parent[] and size[]
    for (int i = 0; i < n; i++) {
        parent[i] = i, size[i] = 1;
    }

    /// Stores the minimum cost
    int ans = 0;

    // Finding the minimum cost
    for (auto x : v) {

        // Perform the union operation
        if (union_sets(x.second.first,
                       x.second.second)) {
            ans += x.first;
        }
    }

    // Print the minimum cost
    cout << ans;
}

// Driver Code
int main()
{
    // Given houses
    int houses[][2] = { { 0, 0 }, { 2, 2 },
                        { 3, 10 }, { 5, 2 },
                        { 7, 0 }};

    int N = sizeof(houses)
            / sizeof(houses[0]);

    // Function Call
    MST(houses, N);

    return 0;
}

Java

// Java program for the above approach
import java.util.*;

// Class for DSU implementation
class DSU{

int parent[];
int rank[];

// Constructor to initialize DSU
DSU(int n)
{
    parent = new int[n];
    rank = new int[n];
    for(int i = 0; i < n; i++)
    {
        parent[i] = -1;
        rank[i] = 1;
    }
}

// Utility function to find set of an
// element v using path compression
// technique
int find_set(int v)
{

    // If v is the parent
    if (parent[v] == -1)
        return v;

    // Otherwise, recursively
    // find its parent
    return parent[v] = find_set(parent[v]);
}

// Function to perform union
// of the sets a and b
void union_sets(int a, int b)
{

    // Find parent of a and b
    int p1 = find_set(a);
    int p2 = find_set(b);

    // If parent are different
    if (p1 != p2)
    {

        // Swap Operation
        if (rank[p1] > rank[p2])
        {
            parent[p2] = p1;
            rank[p1] += rank[p2];
        }
        else
        {
            parent[p1] = p2;
            rank[p2] += rank[p1];
        }
    }
}
}

class GFG{

// Function to create a Minimum Cost
// Spanning tree for given houses
static void MST(int houses[][], int n)
{
    int ans = 0;
    ArrayList<int[]> edges = new ArrayList<>();

    // Traverse each coordinate
    for(int i = 0; i < n; i++)
    {
        for(int j = i + 1; j < n; j++)
        {

            // Find the Manhattan distance
            int p = Math.abs(houses[i][0] -
                             houses[j][0]);

            p += Math.abs(houses[i][1] -
                          houses[j][1]);

            // Add the edges
            edges.add(new int[]{ p, i, j });
        }
    }

    // Sorting arraylist using custome comparator
    // on the basis of weight i.e first element in
    // array object stored in Arraylist
    Collections.sort(edges, new Comparator<int[]>()
    {
        @Override public int compare(int[] o1, int[] o2)
        {
            return Integer.compare(o1[0], o2[0]);
        }
    });

    // Calling DSU class
    DSU d = new DSU(n);
    for(int i = 0; i < edges.size(); i++)
    {
        int from = edges.get(i)[1];
        int to = edges.get(i)[2];

        // Checking if they lie in different component
        // or not i.e they have same parent or not in
        // DSU
        if (d.find_set(from) != d.find_set(to))
        {

            // Calling union_sets
            d.union_sets(from, to);
            ans += edges.get(i)[0];
        }
    }

    // Printing the minimum cost
    System.out.println(ans);
}

// Driver code
public static void main(String args[])
{

    // Graph in form of 2D array
    int houses[][] = { { 0, 0 }, { 2, 2 },
                       { 3, 10 }, { 5, 2 },
                       { 7, 0 } };
    int n = houses.length;

    // Function Call
    MST(houses, n);
}
}

// This code is contributed by Rahul Verma

Python3

# Python3 program for the above approach
parent = [0] * 100
size = [0] * 100

# Utility function to find set of an
# element v using path compression
# technique
def find_set(v):

  #if v is parent
    if (v == parent[v]):
        return v

    # Otherwise, recursively
    # find its parent
    parent[v] = find_set(parent[v])

    return parent[v]

# Function to perform union
# of the sets a and b
def union_sets(a, b):

    # Find parent of a and b
    a = find_set(a)
    b = find_set(b)

    # If parent are different
    if (a != b):

        # Swap Operation
        if (size[a] < size[b]):
            a, b = b, a

        # Update parent of b as a
        parent[b] = a
        size[a] += size[b]
        return 1

    # Otherwise, return 0
    return 0

# Function to create a Minimum Cost
# Spanning tree for given houses
def MST(houses, n):

    # Stores adjacency list of graph
    v = []

    # Traverse each coordinate
    for i in range(n):
        for j in range(i + 1, n):

            # Find the Manhattan distance
            p = abs(houses[i][0] -
                    houses[j][0])

            p += abs(houses[i][1] -
                     houses[j][1])

            # Add the edges
            v.append([p, i, j])

    # Sort all the edges
    v = sorted(v)

    # Initialize parent[] and size[]
    for i in range(n):
        parent[i] = i
        size[i] = 1

    # Stores the minimum cost
    ans = 0

    # Finding the minimum cost
    for x in v:

        # Perform the union operation
        if (union_sets(x[1], x[2])):
            ans += x[0]

    # Print the minimum cost
    print(ans)

# Driver Code
if __name__ == '__main__':

    # Given houses
    houses = [ [ 0, 0 ], [ 2, 2 ],
               [ 3, 10 ], [ 5, 2 ],
               [ 7, 0 ] ]

    N = len(houses)

    # Function Call
    MST(houses, N)

# This code is contributed by mohit kumar 29

Javascript

<script>

// JavaScript program for the above approach
let parent = new Array(100).fill(0)
let size = new Array(100).fill(0)

// Utility function to find set of an
// element v using path compression
// technique
function find_set(v){

    // If v is the parent
    if (v == parent[v])
        return v

    // Otherwise, recursively
    // find its parent
    parent[v] = find_set(parent[v])

    return parent[v]
}

// Function to perform union
// of the sets a and b
function union_sets(a, b){

    // Find parent of a and b
    a = find_set(a)
    b = find_set(b)

    // If parent are different
    if (a != b){

        // Swap Operation
        if (size[a] < size[b]){
            a, b = b, a
        }

        // Update parent of b as a
        parent[b] = a
        size[a] += size[b]
        return 1
    }

    // Otherwise, return 0
    return 0
}

// Function to create a Minimum Cost
// Spanning tree for given houses
function MST(houses, n){

    // Stores adjacency list of graph
    let v = []

    // Traverse each coordinate
    for(let i=0;i<n;i++){
        for(let j=i+1;j<n;j++){

            // Find the Manhattan distance
            let p = Math.abs(houses[i][0] -
                    houses[j][0])

            p += Math.abs(houses[i][1] -
                    houses[j][1])

            // Add the edges
            v.push([p, i, j])
        }
    }

    // Sort all the edges
    v.sort((a,b)=>a[0]-b[0])

    // Initialize parent[] and size[]
    for(let i=0;i<n;i++){
        parent[i] = i
        size[i] = 1
    }

    // Stores the minimum cost
    let ans = 0

    // Finding the minimum cost
    for(let x of v){

        // Perform the union operation
        if (union_sets(x[1], x[2]))
            ans += x[0]

    }

    // Print the minimum cost
    document.write(ans,"</br>")
}

// Driver Code

// Given houses
let houses = [ [ 0, 0 ], [ 2, 2 ], [ 3, 10 ], [ 5, 2 ],[ 7, 0 ] ]

let N = houses.length

// Function Call
MST(houses, N)

// This code is contributed by shinjanpatra

</script>

C#

using System;

class UnionFind
{
    private int[] parent;
    private int[] size;

    public UnionFind(int n)
    {
        parent = new int[n];
        size = new int[n];

        for (int i = 0; i < n; i++)
        {
            parent[i] = i;
            size[i] = 1;
        }
    }
    // Utility function to find set of an
//element v using path compression
// technique

    public int FindSet(int v)
    {
        //if v is parent
        if (v == parent[v])
        {
            return v;
        }
        //Otherwise, recursively
    //find its parent

        parent[v] = FindSet(parent[v]);
        return parent[v];
    }
    // Function to perform union
// of the sets a and b

    public int UnionSets(int a, int b)
    {
         // Find parent of a and b
        a = FindSet(a);
        b = FindSet(b);
 // If parent are different
        if (a != b)
        {
            if (size[a] < size[b])
            {
                 // Swap Operation
                int temp = a;
                a = b;
                b = temp;
            }
            //Update parent of b as a

            parent[b] = a;
            size[a] += size[b];
            return 1;
        }

        return 0;
    }
}

class Program
{
    static void Main(string[] args)
    {
        int[][] houses = new int[][] {
            new int[] { 0, 0 },
            new int[] { 2, 2 },
            new int[] { 3, 10 },
            new int[] { 5, 2 },
            new int[] { 7, 0 }
        };

        int n = houses.Length;

        Tuple<int, int, int>[] edges = new Tuple<int, int, int>[(n * (n - 1)) / 2];
        int count = 0;
         // Traverse each coordinate

        for (int i = 0; i < n; i++)
        {
            for (int j = i + 1; j < n; j++)
            {
                int p = Math.Abs(houses[i][0] - houses[j][0]) +
                        Math.Abs(houses[i][1] - houses[j][1]);
                edges[count++] = Tuple.Create(p, i, j);
            }
        }
        // Sort all the edges

        Array.Sort(edges, (a, b) => a.Item1.CompareTo(b.Item1));

        UnionFind uf = new UnionFind(n);

        int ans = 0;

        foreach (var edge in edges)
        {
            if (uf.UnionSets(edge.Item2, edge.Item3) == 1)
            {
                ans += edge.Item1;
            }
        }

        Console.WriteLine(ans);
    }
}

Output:

20

Time Complexity: O(N²)
Auxiliary Space: O(N²)