Minimum cost to provide water

Given an integer N, where N denotes the number of villages numbered 1 to N, an array wells[] where wells[i] denotes the cost to build a water well in the i‘th city, a 2D array pipes in form of [X Y C] which denotes that the cost to connect village X and Y with water pipes is C. Your task is to provide water to each and every village either by building a well in the village or connecting it to some other village having water. Find the minimum cost to do so.

Examples:

Input: N=3, wells=[1, 2, 2], pipes=[[1 2 1], [2 3 1]]
Output: 3
Explanation: Build well in village1 to provide water with cost=1
connect village2 and village1 with cost =1 , now village1 and village2 have water.
Finally connect village3 with village2 with cost=1 , now all the villages have water with total cost=3.

Input: N=4, wells[1, 1, 1, 1], pipes=[[1 2 100], [2 3 100], [2 4 50]]
Output: 4
Explanation: Clearly its better to construct well at each village rather than building costly roads. Hence total cost=1+1+1+1=4.

Minimum Cost to provide water using Kruskal’s Minimum Spanning Tree (MST) Algorithm & Disjoint Set Union:

We can create a graph with villages as vertices and use pipes array to form edges between these villages, also we need to construct a pseudo vertex that is connected to each and every village ‘i’ with an edges weight of wells[i] , in this way we can take care of cost of building the pipes and wells simultaneously. The MST cost of this graph will give us our answer i.e. the minimum cost to provide water to each village.

Illustration:

Suppose, N=4, wells[1, 2, 1, 2], pipes=[[1 2 1], [1 3 3],[2 3 3], [3 4 1]]
Step 1: We construct the graph with villages as the vertex and use pipes array to form edges as shown in fig-1

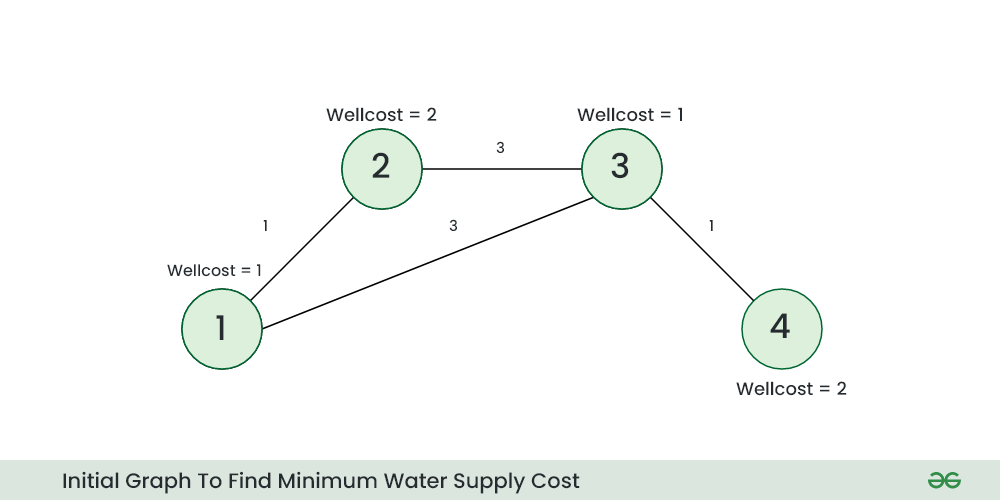
fig-1

Step 2: Create a pseudo node (0) and add edges from 0 to all other vertices from 1 to N , assign edge weight as wells[i] , for each ‘i’ 1 to N.

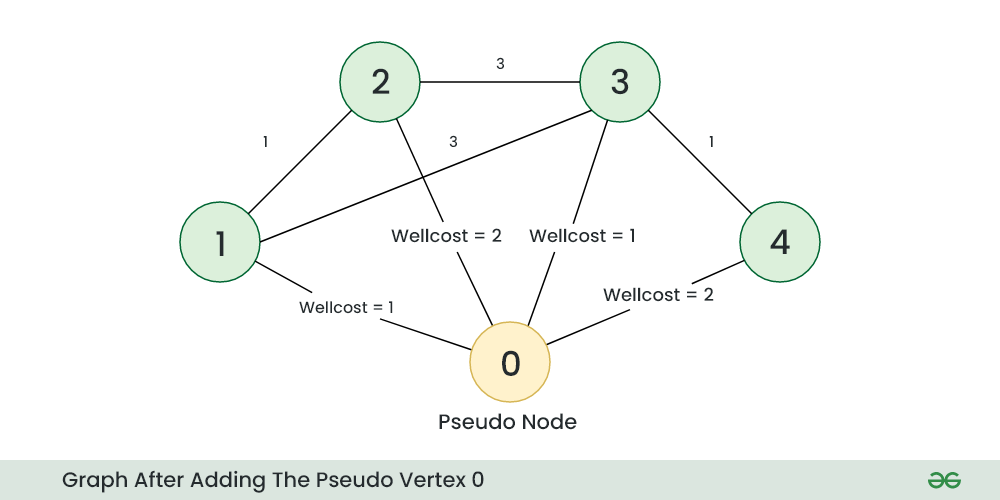
fig-2

Step 3: Find the MST of the above graph and return the MST cost= 1+1+1+1= 4 as the answer.

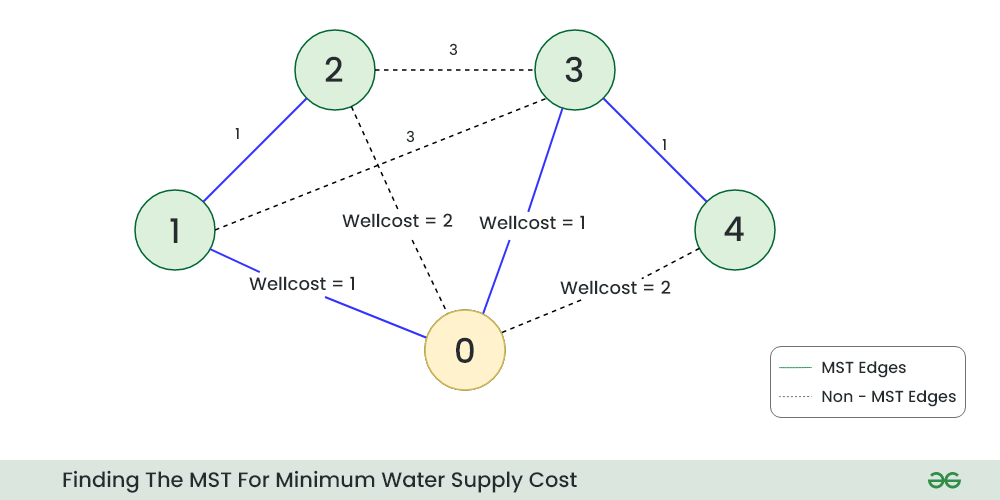
fig-3

Step-by-step algorithm:

• Firstly initialize the DSU data structure i.e. make(), find(), Union(), and parent array.
• Create a set ‘st’ to store the edges sorted in ascending order on the basis of edge weight.
• Insert the edges in ‘st’ using the pipes array.
• Edges between villages(1 to N) and pseudo vertex(0) have to be inserted with edge weight=wells[i] for each village ‘i’.
• Apply Kruskal’s MST algorithm on the set ‘st‘.
• return the MST cost as the answer.

Below is the implementation of the above algorithm:

C++

// C++ code for the above approach:
#include <bits/stdc++.h>
using namespace std;

// Parent array to store parent of
// each component of DSU.
int parent[1001];

// sizez array to apply DSU by size.
int sizez[1001];

// This function is used to initialize
// the DSU.
void make(int i)
{
    parent[i] = i;
    sizez[i] = 1;
}

// This function is used to find the
// parent of each component of DSU
int find(int v)
{
    if (v == parent[v])
        return v;
    return parent[v] = find(parent[v]);
}

// This function is used to merge two
// components of DSU.
void Union(int a, int b)
{

    // Finding the parents of vertex
    // a and b
    a = find(a);
    b = find(b);

    // If parents are not equal
    if (a != b) {
        if (sizez[a] < sizez[b])
            swap(a, b);
        parent[b] = a;

        // Apply DSU by size
        sizez[a] += sizez[b];
    }
}

// Funtion to solve the problem
int minCostToProvideWater(int n, vector<int>& wells,
                          vector<vector<int> >& pipes)
{

    // set to store the edges sorted on
    // the basis of weights.
    set<vector<int> > st;

    // Inserting the edges into the set
    for (auto e : pipes) {
        int u = e[0];
        int v = e[1];
        int wt = e[2];
        st.insert({ wt, u, v });
    }

    // Inserting the edges created by the
    // pseudo vertex i.e. 0
    for (int i = 0; i < n; i++) {
        st.insert({ wells[i], 0, i + 1 });
    }

    // Initializing the DSU
    for (int i = 0; i <= n; i++) {
        make(i);
    }

    int answer = 0;

    // Applying Krushkal's MST algorithm
    while (st.size()) {
        auto it = st.begin();
        int wt = (*it)[0];
        int u = (*it)[1];
        int v = (*it)[2];
        if (find(u) != find(v)) {
            answer += wt;
            Union(u, v);
        }
        st.erase(st.begin());
    }
    return answer;
}

// Driver Function
int main()
{
    int N = 3;
    vector<int> wells = { 1, 2, 2 };
    vector<vector<int> > pipes
        = { { 1, 2, 1 }, { 2, 3, 1 } };

    // Function call
    cout << minCostToProvideWater(N, wells, pipes);
    return 0;
}

Java

// Java program for the above approach

import java.util.*;

public class Main {

    // Parent array to store parent of
    // each component of DSU.
    static int[] parent = new int[1001];

    // sizez array to apply DSU by size.
    static int[] sizez = new int[1001];

    // This function is used to initialize
    // the DSU.
    static void make(int i) {
        parent[i] = i;
        sizez[i] = 1;
    }

    // This function is used to find the
    // parent of each component of DSU
    static int find(int v) {
        if (v == parent[v])
            return v;
        return parent[v] = find(parent[v]);
    }

    // This function is used to merge two
    // components of DSU.
    static void Union(int a, int b) {

        // Finding the parents of vertex
        // a and b
        a = find(a);
        b = find(b);

        // If parents are not equal
        if (a != b) {
            if (sizez[a] < sizez[b]){
                int temp = a;
                a = b;
                b = temp;
            }
            parent[b] = a;

            // Apply DSU by size
            sizez[a] += sizez[b];
        }
    }

    // Function to solve the problem
    static int minCostToProvideWater(int n,
                                     List<Integer> wells,
                                     List<List<Integer>> pipes) {

        // set to store the edges sorted on
        // the basis of weights.
        TreeSet<List<Integer>> st = new TreeSet<>(new Comparator<List<Integer>>() {
            @Override
            public int compare(List<Integer> a, List<Integer> b) {
                return a.get(0).compareTo(b.get(0));
            }
        });

        // Inserting the edges into the set
        for (List<Integer> e : pipes) {
            int u = e.get(0);
            int v = e.get(1);
            int wt = e.get(2);
            st.add(Arrays.asList(wt, u, v));
        }

        // Inserting the edges created by the
        // pseudo vertex i.e. 0
        for (int i = 0; i < n; i++) {
            st.add(Arrays.asList(wells.get(i), 0, i + 1));
        }

        // Initializing the DSU
        for (int i = 0; i <= n; i++) {
            make(i);
        }

        int answer = 0;

        // Applying Kruskal's MST algorithm
        while (!st.isEmpty()) {
            List<Integer> it = st.pollFirst();
            int wt = it.get(0);
            int u = it.get(1);
            int v = it.get(2);
            if (find(u) != find(v)) {
                answer += wt;
                Union(u, v);
            }
        }
        return answer;
    }

    // Driver Function
    public static void main(String[] args) {
        int N = 3;
        List<Integer> wells = Arrays.asList(1, 2, 2);
        List<List<Integer>> pipes = Arrays.asList(
                Arrays.asList(1, 2, 1),
                Arrays.asList(2, 3, 1)
        );

        // Function call
        System.out.println(minCostToProvideWater(N, wells, pipes));
    }
}

// This code is contributed by Abhinav Mahajan (abhinav_m22).

Python3

import heapq

# This function is used to initialize the DSU.
def make(i, parent, sizez):
    parent[i] = i
    sizez[i] = 1

# This function is used to find the parent of each component of DSU
def find(v, parent):
    if v == parent[v]:
        return v
    parent[v] = find(parent[v], parent)
    return parent[v]

# This function is used to merge two components of DSU
def union(a, b, parent, sizez):
    a = find(a, parent)
    b = find(b, parent)
    if a != b:
        if sizez[a] < sizez[b]:
            a, b = b, a
        parent[b] = a
        sizez[a] += sizez[b]

# Function to solve the problem
def min_cost_to_provide_water(n, wells, pipes):
    edges = []

    # Inserting the edges into the heap sorted by weights
    for pipe in pipes:
        u, v, wt = pipe
        edges.append((wt, u, v))

    # Inserting the edges created by the pseudo-vertex i.e., 0
    for i in range(n):
        edges.append((wells[i], 0, i + 1))

    # Initializing DSU
    parent = [0] * (n + 1)
    sizez = [0] * (n + 1)
    for i in range(n + 1):
        make(i, parent, sizez)

    answer = 0

    # Applying Kruskal's MST algorithm
    edges.sort()
    for edge in edges:
        wt, u, v = edge
        if find(u, parent) != find(v, parent):
            answer += wt
            union(u, v, parent, sizez)

    return answer

# Driver Function
if __name__ == "__main__":
    N = 3
    wells = [1, 2, 2]
    pipes = [
        (1, 2, 1),
        (2, 3, 1)
    ]

    # Function call
    print(min_cost_to_provide_water(N, wells, pipes))

C#

using System;
using System.Collections.Generic;

class GFG
{
    // Parent array to store parent of
  // each component of DSU.
    static int[] parent = new int[1001];
    // Size array to apply DSU by size.
    static int[] sizez = new int[1001];
    // This function is used to initialize the DSU.
    static void Make(int i)
    {
        parent[i] = i;
        sizez[i] = 1;
    }
    // This function is used to find the parent of
    // each component of DSU.
    static int Find(int v)
    {
        if (v == parent[v])
            return v;
        return parent[v] = Find(parent[v]);
    }
    // This function is used to merge
    // two components of DSU.
    static void Union(int a, int b)
    {
        // Finding the parents of vertex a and b
        a = Find(a);
        b = Find(b);
        // If parents are not equal
        if (a != b)
        {
            if (sizez[a] < sizez[b])
                (a, b) = (b, a);
            parent[b] = a;
            // Apply DSU by size
            sizez[a] += sizez[b];
        }
    }
    // Function to solve the problem
    static int MinCostToProvideWater(int n, List<int> wells, List<List<int>> pipes)
    {
        // Using SortedSet to store the
        // edges sorted on the basis of weights.
        SortedSet<List<int>> st = new SortedSet<List<int>>(new Geek());
        // Inserting the edges into the set
        foreach (var e in pipes)
        {
            int u = e[0];
            int v = e[1];
            int wt = e[2];
            st.Add(new List<int>() { wt, u, v });
        }
        // Inserting the edges created by the pseudo vertex i.e. 0
        for (int i = 0; i < n; i++)
        {
            st.Add(new List<int>() { wells[i], 0, i + 1 });
        }
        // Initializing the DSU
        for (int i = 0; i <= n; i++)
        {
            Make(i);
        }
        int answer = 0;
        // Applying Kruskal's MST algorithm
        while (st.Count > 0)
        {
            var it = st.Min;
            int wt = it[0];
            int u = it[1];
            int v = it[2];
            if (Find(u) != Find(v))
            {
                answer += wt;
                Union(u, v);
            }
            st.Remove(it);
        }

        return answer;
    }
    // Custom comparer to sort
    // the edges based on weights
    public class Geek : IComparer<List<int>>
    {
        public int Compare(List<int> a, List<int> b)
        {
            return a[0].CompareTo(b[0]);
        }
    }
    // Driver Function
    static void Main()
    {
        int N = 3;
        List<int> wells = new List<int>() { 1, 2, 2 };
        List<List<int>> pipes = new List<List<int>> { new List<int> { 1, 2, 1 }, new List<int> { 2, 3, 1 } };
        // Function call
        Console.WriteLine(MinCostToProvideWater(N, wells, pipes));
    }
}

Javascript

// JavaScript code for the above approach:

// Parent array to store parent of
// each component of DSU.
let parent = new Array(1001);
// sizez array to apply DSU by size.
let sizez = new Array(1001);
// This function is used to initialize
// the DSU.
function make(i) {
  parent[i] = i;
  sizez[i] = 1;
}
// This function is used to find the
// parent of each component of DSU
function find(v) {
  if (v == parent[v])
    return v;
  return parent[v] = find(parent[v]);
}

// This function is used to merge two
// components of DSU.
function Union(a, b) {

  // Finding the parents of vertex
  // a and b
  a = find(a);
  b = find(b);

  // If parents are not equal
  if (a != b) {
    if (sizez[a] < sizez[b])
      [a, b] = [b, a];
    parent[b] = a;

    // Apply DSU by size
    sizez[a] += sizez[b];
  }
}

// Funtion to solve the problem
function minCostToProvideWater(n, wells, pipes) {

   // set to store the edges sorted on
    // the basis of weights.
  let st = new Set();


  // Inserting the edges into the set
  for (let e of pipes) {
    let u = e[0];
    let v = e[1];
    let wt = e[2];
    st.add([wt, u, v]);
  }


  // Inserting the edges created by the
    // pseudo vertex i.e. 0
  for (let i = 0; i < n; i++) {
    st.add([wells[i], 0, i + 1]);
  }

  // Initializing the DSU
  for (let i = 0; i <= n; i++) {
    make(i);
  }
  let answer = 0;

  // Applying Krushkal's MST algorithm
  while (st.size) {
    let it = st.values().next().value;
    let wt = it[0];
    let u = it[1];
    let v = it[2];
    if (find(u) != find(v)) {
      answer += wt;
      Union(u, v);
    }
    st.delete(it);
  }
  return answer;
}
let N = 3;
let wells = [1, 2, 2];
let pipes = [[1, 2, 1], [2, 3, 1]];
console.log(minCostToProvideWater(N, wells, pipes));

Output

3

Time Complexity: O(E*log(N)), where E is the number of edges and N is the number of vertices in the formed graph.
Auxiliary Space: O(N)