Minimum cost to connect all cities

There are n cities and there are roads in between some of the cities. Somehow all the roads are damaged simultaneously. We have to repair the roads to connect the cities again. There is a fixed cost to repair a particular road. Find out the minimum cost to connect all the cities by repairing roads. Input is in matrix(city) form, if city[i][j] = 0 then there is not any road between city i and city j, if city[i][j] = a > 0 then the cost to rebuild the path between city i and city j is a. Print out the minimum cost to connect all the cities. 
It is sure that all the cities were connected before the roads were damaged.

Examples:

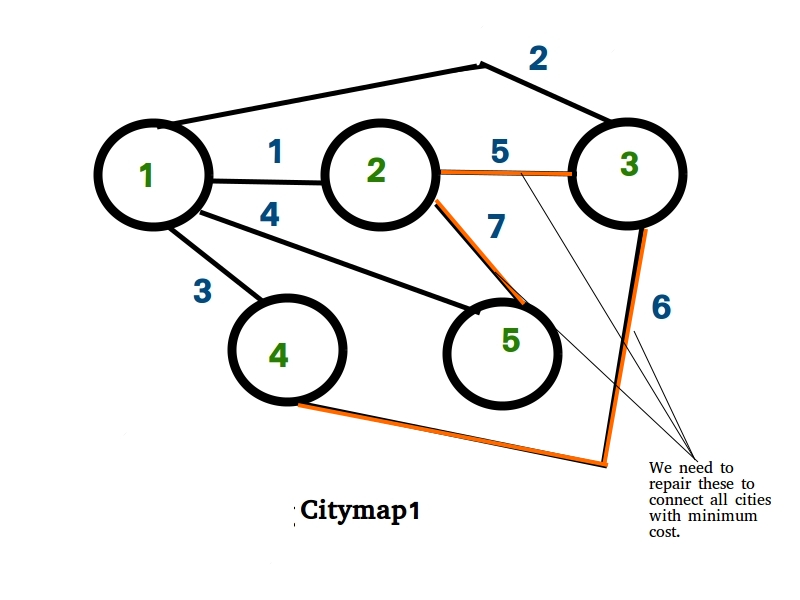
Input : {{0, 1, 2, 3, 4},
         {1, 0, 5, 0, 7},
         {2, 5, 0, 6, 0},
         {3, 0, 6, 0, 0},
         {4, 7, 0, 0, 0}};
Output : 10

Input : {{0, 1, 1, 100, 0, 0},
         {1, 0, 1, 0, 0, 0},
         {1, 1, 0, 0, 0, 0},
         {100, 0, 0, 0, 2, 2},
         {0, 0, 0, 2, 0, 2},
         {0, 0, 0, 2, 2, 0}};
Output : 106

Method: Here we have to connect all the cities by path which will cost us least. The way to do that is to find out the Minimum Spanning Tree(MST) of the map of the cities(i.e. each city is a node of the graph and all the damaged roads between cities are edges). And the total cost is the addition of the path edge values in the Minimum Spanning Tree.

Prerequisite: MST Prim’s Algorithm

Implementation:

C++

// C++ code to find out minimum cost
// path to connect all the cities
#include <bits/stdc++.h>

using namespace std;

// Function to find out minimum valued node
// among the nodes which are not yet included in MST
int minnode(int n, int keyval[], bool mstset[]) {
  int mini = numeric_limits<int>::max();
  int mini_index;

  // Loop through all the values of the nodes
  // which are not yet included in MST and find
  // the minimum valued one.
  for (int i = 0; i < n; i++) {
    if (mstset[i] == false && keyval[i] < mini) {
      mini = keyval[i], mini_index = i;
    }
  }
  return mini_index;
}

// Function to find out the MST and
// the cost of the MST.
void findcost(int n, vector<vector<int>> city) {

  // Array to store the parent node of a
  // particular node.
  int parent[n];

  // Array to store key value of each node.
  int keyval[n];

  // Boolean Array to hold bool values whether
  // a node is included in MST or not.
  bool mstset[n];

  // Set all the key values to infinite and
  // none of the nodes is included in MST.
  for (int i = 0; i < n; i++) {
    keyval[i] = numeric_limits<int>::max();
    mstset[i] = false;
  }

  // Start to find the MST from node 0.
  // Parent of node 0 is none so set -1.
  // key value or minimum cost to reach
  // 0th node from 0th node is 0.
  parent[0] = -1;
  keyval[0] = 0;

  // Find the rest n-1 nodes of MST.
  for (int i = 0; i < n - 1; i++) {

    // First find out the minimum node
    // among the nodes which are not yet
    // included in MST.
    int u = minnode(n, keyval, mstset);

    // Now the uth node is included in MST.
    mstset[u] = true;

    // Update the values of neighbor
    // nodes of u which are not yet
    // included in MST.
    for (int v = 0; v < n; v++) {

      if (city[u][v] && mstset[v] == false &&
          city[u][v] < keyval[v]) {
        keyval[v] = city[u][v];
        parent[v] = u;
      }
    }
  }

  // Find out the cost by adding
  // the edge values of MST.
  int cost = 0;
  for (int i = 1; i < n; i++)
    cost += city[parent[i]][i];
  cout << cost << endl;
}

// Utility Program:
int main() {

  // Input 1
  int n1 = 5;
  vector<vector<int>> city1 = {{0, 1, 2, 3, 4},
                               {1, 0, 5, 0, 7},
                               {2, 5, 0, 6, 0},
                               {3, 0, 6, 0, 0},
                               {4, 7, 0, 0, 0}};
  findcost(n1, city1);

  // Input 2
  int n2 = 6;
  vector<vector<int>> city2 = {{0, 1, 1, 100, 0, 0},
                               {1, 0, 1, 0, 0, 0},
                               {1, 1, 0, 0, 0, 0},
                               {100, 0, 0, 0, 2, 2},
                               {0, 0, 0, 2, 0, 2},
                               {0, 0, 0, 2, 2, 0}};
  findcost(n2, city2);

  return 0;
}

Java

// Java code to find out minimum cost
// path to connect all the cities
import java.util.*;

class GFG{

// Function to find out minimum valued node
// among the nodes which are not yet included
// in MST
static int minnode(int n, int keyval[],
                   boolean mstset[])
{
    int mini = Integer.MAX_VALUE;
    int mini_index = 0;

    // Loop through all the values of the nodes
    // which are not yet included in MST and find
    // the minimum valued one.
    for(int i = 0; i < n; i++)
    {
        if (mstset[i] == false &&
            keyval[i] < mini)
        {
            mini = keyval[i];
            mini_index = i;
        }
    }
    return mini_index;
}

// Function to find out the MST and
// the cost of the MST.
static void findcost(int n, int city[][])
{

    // Array to store the parent node of a
    // particular node.
    int parent[] = new int[n];

    // Array to store key value of each node.
    int keyval[] = new int[n];

    // Boolean Array to hold bool values whether
    // a node is included in MST or not.
    boolean mstset[] = new boolean[n];

    // Set all the key values to infinite and
    // none of the nodes is included in MST.
    for(int i = 0; i < n; i++)
    {
        keyval[i] = Integer.MAX_VALUE;
        mstset[i] = false;
    }

    // Start to find the MST from node 0.
    // Parent of node 0 is none so set -1.
    // key value or minimum cost to reach
    // 0th node from 0th node is 0.
    parent[0] = -1;
    keyval[0] = 0;

    // Find the rest n-1 nodes of MST.
    for(int i = 0; i < n - 1; i++)
    {

        // First find out the minimum node
        // among the nodes which are not yet
        // included in MST.
        int u = minnode(n, keyval, mstset);

        // Now the uth node is included in MST.
        mstset[u] = true;

        // Update the values of neighbor
        // nodes of u which are not yet
        // included in MST.
        for(int v = 0; v < n; v++)
        {
            if (city[u][v] > 0 &&
                 mstset[v] == false &&
                city[u][v] < keyval[v])
            {
                keyval[v] = city[u][v];
                parent[v] = u;
            }
        }
    }

    // Find out the cost by adding
    // the edge values of MST.
    int cost = 0;
    for(int i = 1; i < n; i++)
        cost += city[parent[i]][i];

    System.out.println(cost);
}

// Driver code
public static void main(String args[])
{

    // Input 1
    int n1 = 5;
    int city1[][] = { { 0, 1, 2, 3, 4 },
                      { 1, 0, 5, 0, 7 },
                      { 2, 5, 0, 6, 0 },
                      { 3, 0, 6, 0, 0 },
                      { 4, 7, 0, 0, 0 } };

    findcost(n1, city1);

    // Input 2
    int n2 = 6;
    int city2[][] = { { 0, 1, 1, 100, 0, 0 },
                      { 1, 0, 1, 0, 0, 0 },
                      { 1, 1, 0, 0, 0, 0 },
                      { 100, 0, 0, 0, 2, 2 },
                      { 0, 0, 0, 2, 0, 2 },
                      { 0, 0, 0, 2, 2, 0 } };

    findcost(n2, city2);

}
}

// This code is contributed by adityapande88

Python3

# Python3 code to find out minimum cost
# path to connect all the cities

# Function to find out minimum valued
# node among the nodes which are not
# yet included in MST
def minnode(n, keyval, mstset):
    mini = 999999999999
    mini_index = None

    # Loop through all the values of
    # the nodes which are not yet
    # included in MST and find the
    # minimum valued one.
    for i in range(n):
        if (mstset[i] == False and
            keyval[i] < mini):
            mini = keyval[i]
            mini_index = i
    return mini_index

# Function to find out the MST and
# the cost of the MST.
def findcost(n, city):

    # Array to store the parent
    # node of a particular node.
    parent = [None] * n

    # Array to store key value
    # of each node.
    keyval = [None] * n

    # Boolean Array to hold bool
    # values whether a node is
    # included in MST or not.
    mstset = [None] * n

    # Set all the key values to infinite and
    # none of the nodes is included in MST.
    for i in range(n):
        keyval[i] = 9999999999999
        mstset[i] = False

    # Start to find the MST from node 0.
    # Parent of node 0 is none so set -1.
    # key value or minimum cost to reach
    # 0th node from 0th node is 0.
    parent[0] = -1
    keyval[0] = 0

    # Find the rest n-1 nodes of MST.
    for i in range(n - 1):

        # First find out the minimum node
        # among the nodes which are not yet
        # included in MST.
        u = minnode(n, keyval, mstset)

        # Now the uth node is included in MST.
        mstset[u] = True

        # Update the values of neighbor
        # nodes of u which are not yet
        # included in MST.
        for v in range(n):
            if (city[u][v] and mstset[v] == False and
                city[u][v] < keyval[v]):
                keyval[v] = city[u][v]
                parent[v] = u

    # Find out the cost by adding
    # the edge values of MST.
    cost = 0
    for i in range(1, n):
        cost += city[parent[i]][i]
    print(cost)

# Driver Code
if __name__ == '__main__':

    # Input 1
    n1 = 5
    city1 = [[0, 1, 2, 3, 4],
             [1, 0, 5, 0, 7],
             [2, 5, 0, 6, 0],
             [3, 0, 6, 0, 0],
             [4, 7, 0, 0, 0]]
    findcost(n1, city1)

    # Input 2
    n2 = 6
    city2 = [[0, 1, 1, 100, 0, 0],
             [1, 0, 1, 0, 0, 0],
             [1, 1, 0, 0, 0, 0],
             [100, 0, 0, 0, 2, 2],
             [0, 0, 0, 2, 0, 2],
             [0, 0, 0, 2, 2, 0]]
    findcost(n2, city2)

# This code is contributed by PranchalK

C#

// C# code to find out minimum cost
// path to connect all the cities
using System;

class GFG{

// Function to find out minimum valued node
// among the nodes which are not yet included
// in MST
static int minnode(int n, int[] keyval,
                   bool[] mstset)
{
    int mini = Int32.MaxValue;
    int mini_index = 0;

    // Loop through all the values of the nodes
    // which are not yet included in MST and find
    // the minimum valued one.
    for(int i = 0; i < n; i++)
    {
        if (mstset[i] == false && keyval[i] < mini)
        {
            mini = keyval[i];
            mini_index = i;
        }
    }
    return mini_index;
}

// Function to find out the MST and
// the cost of the MST.
static void findcost(int n, int[,] city)
{

    // Array to store the parent node of a
    // particular node.
    int[] parent = new int[n];

    // Array to store key value of each node.
    int[] keyval = new int[n];

    // Boolean Array to hold bool values whether
    // a node is included in MST or not.
    bool[] mstset = new bool[n];

    // Set all the key values to infinite and
    // none of the nodes is included in MST.
    for(int i = 0; i < n; i++)
    {
        keyval[i] = Int32.MaxValue;
        mstset[i] = false;
    }

    // Start to find the MST from node 0.
    // Parent of node 0 is none so set -1.
    // key value or minimum cost to reach
    // 0th node from 0th node is 0.
    parent[0] = -1;
    keyval[0] = 0;

    // Find the rest n-1 nodes of MST.
    for(int i = 0; i < n - 1; i++)
    {

        // First find out the minimum node
        // among the nodes which are not yet
        // included in MST.
        int u = minnode(n, keyval, mstset);

        // Now the uth node is included in MST.
        mstset[u] = true;

        // Update the values of neighbor
        // nodes of u which are not yet
        // included in MST.
        for(int v = 0; v < n; v++)
        {
            if (city[u, v] > 0 && mstset[v] == false &&
                city[u, v] < keyval[v])
            {
                keyval[v] = city[u, v];
                parent[v] = u;
            }
        }
    }

    // Find out the cost by adding
    // the edge values of MST.
    int cost = 0;
    for(int i = 1; i < n; i++)
        cost += city[parent[i], i];

    Console.WriteLine(cost);
}

// Driver code
public static void Main(string[] args)
{

    // Input 1
    int n1 = 5;
    int[,] city1 = { { 0, 1, 2, 3, 4 },
                     { 1, 0, 5, 0, 7 },
                     { 2, 5, 0, 6, 0 },
                     { 3, 0, 6, 0, 0 },
                     { 4, 7, 0, 0, 0 } };

    findcost(n1, city1);

    // Input 2
    int n2 = 6;
    int[,] city2 = { { 0, 1, 1, 100, 0, 0 },
                     { 1, 0, 1, 0, 0, 0 },
                     { 1, 1, 0, 0, 0, 0 },
                     { 100, 0, 0, 0, 2, 2 },
                     { 0, 0, 0, 2, 0, 2 },
                     { 0, 0, 0, 2, 2, 0 } };

    findcost(n2, city2);
}
}

// This code is contributed by ukasp

Javascript

<script>

// Javascript code to find out minimum cost
// path to connect all the cities

// Function to find out minimum valued node
// among the nodes which are not yet included
// in MST
function minnode(n, keyval,
                   mstset)
{
    let mini = Number.MAX_VALUE;
    let mini_index = 0;

    // Loop through all the values of the nodes
    // which are not yet included in MST and find
    // the minimum valued one.
    for(let i = 0; i < n; i++)
    {
        if (mstset[i] == false &&
            keyval[i] < mini)
        {
            mini = keyval[i];
            mini_index = i;
        }
    }
    return mini_index;
}

// Function to find out the MST and
// the cost of the MST.
function findcost(n, city)
{

    // Array to store the parent node of a
    // particular node.
    let parent = Array(n).fill(0);

    // Array to store key value of each node.
    let keyval = Array(n).fill(0);

    // Boolean Array to hold bool values whether
    // a node is included in MST or not.
    let mstset = Array(n).fill(0);

    // Set all the key values to infinite and
    // none of the nodes is included in MST.
    for(let i = 0; i < n; i++)
    {
        keyval[i] = Number.MAX_VALUE;
        mstset[i] = false;
    }

    // Start to find the MST from node 0.
    // Parent of node 0 is none so set -1.
    // key value or minimum cost to reach
    // 0th node from 0th node is 0.
    parent[0] = -1;
    keyval[0] = 0;

    // Find the rest n-1 nodes of MST.
    for(let i = 0; i < n - 1; i++)
    {

        // First find out the minimum node
        // among the nodes which are not yet
        // included in MST.
        let u = minnode(n, keyval, mstset);

        // Now the uth node is included in MST.
        mstset[u] = true;

        // Update the values of neighbor
        // nodes of u which are not yet
        // included in MST.
        for(let v = 0; v < n; v++)
        {
            if (city[u][v] > 0 &&
                 mstset[v] == false &&
                city[u][v] < keyval[v])
            {
                keyval[v] = city[u][v];
                parent[v] = u;
            }
        }
    }

    // Find out the cost by adding
    // the edge values of MST.
    let cost = 0;
    for(let i = 1; i < n; i++)
        cost += city[parent[i]][i];

    document.write(cost + "<br/>") ;
}

// driver code

        // Input 1
    let n1 = 5;
    let city1 =     [[ 0, 1, 2, 3, 4 ],
                      [ 1, 0, 5, 0, 7 ],
                      [ 2, 5, 0, 6, 0 ],
                      [ 3, 0, 6, 0, 0 ],
                      [ 4, 7, 0, 0, 0 ]];

    findcost(n1, city1);

    // Input 2
    let n2 = 6;
    let city2 = [[ 0, 1, 1, 100, 0, 0 ],
                      [ 1, 0, 1, 0, 0, 0 ],
                      [ 1, 1, 0, 0, 0, 0 ],
                      [ 100, 0, 0, 0, 2, 2 ],
                      [ 0, 0, 0, 2, 0, 2 ],
                      [ 0, 0, 0, 2, 2, 0 ]];

    findcost(n2, city2);

</script>

Output:

10
106

Time Complexity: The outer loop(i.e. the loop to add new node to MST) runs n times and in each iteration of the loop it takes O(n) time to find the min node and O(n) time to update the neighboring nodes of u-th node. Hence the overall complexity is O(n²)

Auxiliary Space: O(n)