Minimum Cost to cut a board into squares

Difficulty Level : Hard
Last Updated : 20 May, 2021

A board of length m and width n is given, we need to break this board into m*n squares such that cost of breaking is minimum. cutting cost for each edge will be given for the board. In short, we need to choose such a sequence of cutting such that cost is minimized.
Examples:

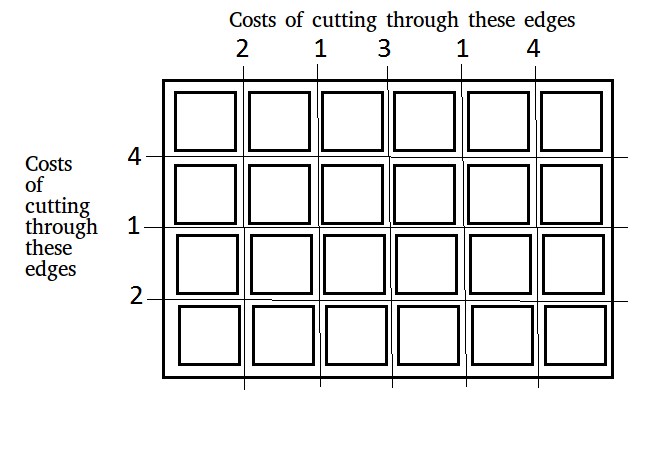
For above board optimal way to cut into square is:
Total minimum cost in above case is 42. It is 
evaluated using following steps.

Initial Value : Total_cost = 0
Total_cost = Total_cost + edge_cost * total_pieces

Cost 4 Horizontal cut         Cost = 0 + 4*1 = 4
Cost 4 Vertical cut        Cost = 4 + 4*2 = 12
Cost 3 Vertical cut        Cost = 12 + 3*2 = 18
Cost 2 Horizontal cut        Cost = 18 + 2*3 = 24
Cost 2 Vertical cut        Cost = 24 + 2*3 = 30
Cost 1 Horizontal cut        Cost = 30 + 1*4 = 34
Cost 1 Vertical cut        Cost = 34 + 1*4 = 38
Cost 1 Vertical cut        Cost = 38 + 1*4 = 42

This problem can be solved using greedy approach, If total cost is denoted by S, then S = a1w1 + a2w2 … + akwk, where wi is a cost of certain edge cutting and ai is corresponding coefficient, The coefficient ai is determined by the total number of cuts we have competed using edge wi at the end of the cutting process. Notice that sum of the coefficients is always constant, hence we want to find a distribution of ai obtainable such that S is minimum. To do so we perform cuts on highest cost edge as early as possible, which will reach to optimal S. If we encounter several edges having the same cost, we can cut any one of them first.
Below is the solution using above approach, first we sorted the edge cutting costs in reverse order, then we loop in them from higher-cost to lower-cost building our solution. Each time we choose an edge, counterpart count is incremented by 1, which is to be multiplied each time with corresponding edge cutting cost.
Notice below used sort method, sending greater() as 3rd argument to sort method sorts number in non-increasing order, it is predefined function of the library.

C++

//  C++ program to divide a board into m*n squares
#include <bits/stdc++.h>
using namespace std;
 
// method returns minimum cost to break board into
// m*n squares
int minimumCostOfBreaking(int X[], int Y[], int m, int n)
{
    int res = 0;
 
    //  sort the horizontal cost in reverse order
    sort(X, X + m, greater<int>());
 
    //  sort the vertical cost in reverse order
    sort(Y, Y + n, greater<int>());
 
    //  initialize current width as 1
    int hzntl = 1, vert = 1;
 
    //  loop untill one or both cost array are processed
    int i = 0, j = 0;
    while (i < m && j < n)
    {
        if (X[i] > Y[j])
        {
            res += X[i] * vert;
 
            //  increase current horizontal part count by 1
            hzntl++;
            i++;
        }
        else
        {
            res += Y[j] * hzntl;
 
            //  increase current vertical part count by 1
            vert++;
            j++;
        }
    }
 
    // loop for horizontal array, if remains
    int total = 0;
    while (i < m)
        total += X[i++];
    res += total * vert;
 
    // loop for vertical array, if remains
    total = 0;
    while (j < n)
        total += Y[j++];
    res += total * hzntl;
 
    return res;
}
 
//  Driver code to test above methods
int main()
{
    int m = 6, n = 4;
    int X[m-1] = {2, 1, 3, 1, 4};
    int Y[n-1] = {4, 1, 2};
    cout << minimumCostOfBreaking(X, Y, m-1, n-1);
    return 0;
}

Java

// Java program to divide a
// board into m*n squares
import java.util.Arrays;
import java.util.Collections;
 
class GFG
{
    // method returns minimum cost to break board into
    // m*n squares
    static int minimumCostOfBreaking(Integer X[], Integer Y[],
                                                 int m, int n)
    {
        int res = 0;
     
        // sort the horizontal cost in reverse order
        Arrays.sort(X, Collections.reverseOrder());
     
        // sort the vertical cost in reverse order
        Arrays.sort(Y, Collections.reverseOrder());
     
        // initialize current width as 1
        int hzntl = 1, vert = 1;
     
        // loop untill one or both
        // cost array are processed
        int i = 0, j = 0;
        while (i < m && j < n)
        {
            if (X[i] > Y[j])
            {
                res += X[i] * vert;
     
                // increase current horizontal
                // part count by 1
                hzntl++;
                i++;
            }
            else
            {
                res += Y[j] * hzntl;
     
                // increase current vertical
                // part count by 1
                vert++;
                j++;
            }
        }
     
        // loop for horizontal array,
        // if remains
        int total = 0;
        while (i < m)
            total += X[i++];
        res += total * vert;
     
        // loop for vertical array,
        // if remains
        total = 0;
        while (j < n)
            total += Y[j++];
        res += total * hzntl;
     
        return res;
    }
     
    // Driver program
    public static void main(String arg[])
    {
        int m = 6, n = 4;
        Integer X[] = {2, 1, 3, 1, 4};
        Integer Y[] = {4, 1, 2};
        System.out.print(minimumCostOfBreaking(X, Y, m-1, n-1));
    }
}
 
// This code is contributed by Anant Agarwal.

Python3

# Python program to divide a board into m*n squares
 
# Method returns minimum cost to 
# break board into m*n squares
def minimumCostOfBreaking(X, Y, m, n):
 
    res = 0
 
    # sort the horizontal cost in reverse order
    X.sort(reverse = True)
 
    # sort the vertical cost in reverse order
    Y.sort(reverse = True)
 
    # initialize current width as 1
    hzntl = 1; vert = 1
 
    # loop untill one or both
    # cost array are processed
    i = 0; j = 0
    while (i < m and j < n):
     
        if (X[i] > Y[j]):
         
            res += X[i] * vert
 
            # increase current horizontal
            # part count by 1
            hzntl += 1
            i += 1
         
        else:
            res += Y[j] * hzntl
 
            # increase current vertical
            # part count by 1
            vert += 1
            j += 1
 
    # loop for horizontal array, if remains
    total = 0
    while (i < m):
        total += X[i]
        i += 1
    res += total * vert
 
    #loop for vertical array, if remains
    total = 0
    while (j < n):
        total += Y[j]
        j += 1
    res += total * hzntl
 
    return res
     
# Driver program
m = 6; n = 4
X = [2, 1, 3, 1, 4]
Y = [4, 1, 2]
 
print(minimumCostOfBreaking(X, Y, m-1, n-1))
 
 
# This code is contributed by Anant Agarwal.

C#

// C# program to divide a
// board into m*n squares
using System;
 
class GFG
{
    // method returns minimum cost to break board into
    // m*n squares
    static int minimumCostOfBreaking(int[] X, int[] Y,
                                        int m, int n)
    {
        int res = 0;
     
        // sort the horizontal cost in reverse order
        Array.Sort<int>(X, new Comparison<int>(
                (i1, i2) => i2.CompareTo(i1)));
     
        // sort the vertical cost in reverse order
        Array.Sort<int>(Y, new Comparison<int>(
                (i1, i2) => i2.CompareTo(i1)));
     
        // initialize current width as 1
        int hzntl = 1, vert = 1;
     
        // loop untill one or both
        // cost array are processed
        int i = 0, j = 0;
        while (i < m && j < n)
        {
            if (X[i] > Y[j])
            {
                res += X[i] * vert;
     
                // increase current horizontal
                // part count by 1
                hzntl++;
                i++;
            }
            else
            {
                res += Y[j] * hzntl;
     
                // increase current vertical
                // part count by 1
                vert++;
                j++;
            }
        }
     
        // loop for horizontal array,
        // if remains
        int total = 0;
        while (i < m)
            total += X[i++];
        res += total * vert;
     
        // loop for vertical array,
        // if remains
        total = 0;
        while (j < n)
            total += Y[j++];
        res += total * hzntl;
     
        return res;
    }
     
    // Driver program
    public static void Main(String []arg)
    {
        int m = 6, n = 4;
        int []X = {2, 1, 3, 1, 4};
        int []Y = {4, 1, 2};
        Console.WriteLine(minimumCostOfBreaking(X, Y, m-1, n-1));
    }
}
 
// This code is contributed by Princi Singh

Javascript

<script>
 
// JavaScript program to divide a
// board into m*n squares
 
    // method returns minimum cost to break board leto
    // m*n squares
    function minimumCostOfBreaking(X, Y,  m, n)
    {
        let res = 0;
       
        // sort the horizontal cost in reverse order
        X.sort();
        X.reverse();
       
        // sort the vertical cost in reverse order
        Y.sort();
        Y.reverse();
       
        // initialize current width as 1
        let hzntl = 1, vert = 1;
       
        // loop untill one or both
        // cost array are processed
        let i = 0, j = 0;
        while (i < m && j < n)
        {
            if (X[i] > Y[j])
            {
                res += X[i] * vert;
       
                // increase current horizontal
                // part count by 1
                hzntl++;
                i++;
            }
            else
            {
                res += Y[j] * hzntl;
       
                // increase current vertical
                // part count by 1
                vert++;
                j++;
            }
        }
       
        // loop for horizontal array,
        // if remains
        let total = 0;
        while (i < m)
            total += X[i++];
        res += total * vert;
       
        // loop for vertical array,
        // if remains
        total = 0;
        while (j < n)
            total += Y[j++];
        res += total * hzntl;
       
        return res;
    }
       
 
// Driver Code
 
        let m = 6, n = 4;
        let X = [2, 1, 3, 1, 4];
        let Y = [4, 1, 2];
        document.write(minimumCostOfBreaking(X, Y, m-1, n-1));
      
</script>

Output:

This article is contributed by Utkarsh Trivedi. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live

My Personal Notes

Related Articles

C++

Java

Python3

C#

Javascript