Merge two binary Max Heaps

Given two binary max heaps as arrays, the task is to merge the given heaps.

Examples :

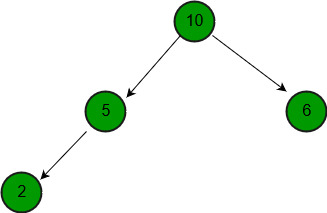
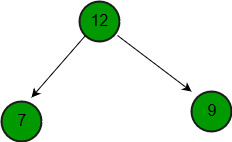
Input: a = {10, 5, 6, 2}, b = {12, 7, 9}
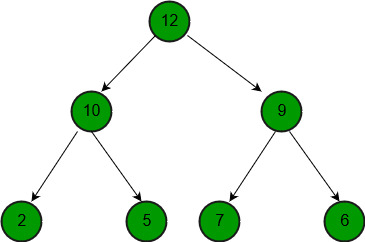
Output: {12, 10, 9, 2, 5, 7, 6}

Input: a = {2, 5, 1, 9, 12}, b = {3, 7, 4, 10}
Output: {12, 10, 7, 9, 5, 3, 1, 4, 2}

Approach:To solve the problem follow the below idea:

Create an array to store the result. Copy both given arrays one by one into result. Once all the elements have been copied, then call standard build heap to construct full merged max heap. 

Follow the given steps to solve the problem:

• Create an array merged of size N+M
• Copy elements of both the arrays in the array merged
• Build Max-Heap of this array
• Print elements of the Max-Heap

Below is the implementation of the above approach:

C++

// C++ program to merge two max heaps.
#include <bits/stdc++.h>
using namespace std;

// Standard heapify function to heapify a
// subtree rooted under idx. It assumes
// that subtrees of node are already heapified.
void maxHeapify(int arr[], int N, int idx)
{
    // Find largest of node and its children
    if (idx >= N)
        return;

    int l = 2 * idx + 1;
    int r = 2 * idx + 2;
    int max = idx;
    if (l < N && arr[l] > arr[idx])
        max = l;
    if (r < N && arr[r] > arr[max])
        max = r;

    // Put maximum value at root and
    // recur for the child with the
    // maximum value
    if (max != idx) {
        swap(arr[max], arr[idx]);
        maxHeapify(arr, N, max);
    }
}

// Builds a max heap of given arr[0..n-1]
void buildMaxHeap(int arr[], int N)
{
    // building the heap from first non-leaf
    // node by calling max heapify function
    for (int i = N / 2 - 1; i >= 0; i--)
        maxHeapify(arr, N, i);
}

// Merges max heaps a[] and b[] into merged[]
void mergeHeaps(int merged[], int a[], int b[], int N,
                int M)
{
    // Copy elements of a[] and b[] one by one
    // to merged[]
    for (int i = 0; i < N; i++)
        merged[i] = a[i];
    for (int i = 0; i < M; i++)
        merged[N + i] = b[i];

    // build heap for the modified array of
    // size n+m
    buildMaxHeap(merged, N + M);
}

// Driver's code
int main()
{
    int a[] = { 10, 5, 6, 2 };
    int b[] = { 12, 7, 9 };

    int N = sizeof(a) / sizeof(a[0]);
    int M = sizeof(b) / sizeof(b[0]);

    int merged[N + M];

    // Function call
    mergeHeaps(merged, a, b, N, M);

    for (int i = 0; i < N + M; i++)
        cout << merged[i] << " ";

    return 0;
}

C

// C program to merge two max heaps.
#include <stdio.h>

void swap(int* a, int* b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

// Standard heapify function to heapify a
// subtree rooted under idx. It assumes
// that subtrees of node are already heapified.
void maxHeapify(int arr[], int N, int idx)
{
    // Find largest of node and its children
    if (idx >= N)
        return;

    int l = 2 * idx + 1;
    int r = 2 * idx + 2;
    int max = idx;
    if (l < N && arr[l] > arr[idx])
        max = l;
    if (r < N && arr[r] > arr[max])
        max = r;

    // Put maximum value at root and
    // recur for the child with the
    // maximum value
    if (max != idx) {
        swap(&arr[max], &arr[idx]);
        maxHeapify(arr, N, max);
    }
}

// Builds a max heap of given arr[0..n-1]
void buildMaxHeap(int arr[], int N)
{
    // building the heap from first non-leaf
    // node by calling max heapify function
    for (int i = N / 2 - 1; i >= 0; i--)
        maxHeapify(arr, N, i);
}

// Merges max heaps a[] and b[] into merged[]
void mergeHeaps(int merged[], int a[], int b[], int N,
                int M)
{
    // Copy elements of a[] and b[] one by one
    // to merged[]
    for (int i = 0; i < N; i++)
        merged[i] = a[i];
    for (int i = 0; i < M; i++)
        merged[N + i] = b[i];

    // build heap for the modified array of
    // size n+m
    buildMaxHeap(merged, N + M);
}

// Driver's code
int main()
{
    int a[] = { 10, 5, 6, 2 };
    int b[] = { 12, 7, 9 };

    int N = sizeof(a) / sizeof(a[0]);
    int M = sizeof(b) / sizeof(b[0]);

    int merged[N + M];

    // Function call
    mergeHeaps(merged, a, b, N, M);

    for (int i = 0; i < N + M; i++)
        printf("%d ", merged[i]);

    return 0;
}

Java

// Java program to merge two max heaps.

class GfG {

    // Standard heapify function to heapify a
    // subtree rooted under idx. It assumes
    // that subtrees of node are already heapified.
    public static void maxHeapify(int[] arr, int N, int i)
    {
        // Find largest of node and its children
        if (i >= N) {
            return;
        }
        int l = i * 2 + 1;
        int r = i * 2 + 2;
        int max;
        if (l < N && arr[l] > arr[i]) {
            max = l;
        }
        else
            max = i;
        if (r < N && arr[r] > arr[max]) {
            max = r;
        }

        // Put maximum value at root and
        // recur for the child with the
        // maximum value
        if (max != i) {
            int temp = arr[max];
            arr[max] = arr[i];
            arr[i] = temp;
            maxHeapify(arr, N, max);
        }
    }

    // Merges max heaps a[] and b[] into merged[]
    public static void mergeHeaps(int[] arr, int[] a,
                                  int[] b, int N, int M)
    {
        for (int i = 0; i < N; i++) {
            arr[i] = a[i];
        }
        for (int i = 0; i < M; i++) {
            arr[N + i] = b[i];
        }
        N = N + M;

        // Builds a max heap of given arr[0..n-1]
        for (int i = N / 2 - 1; i >= 0; i--) {
            maxHeapify(arr, N, i);
        }
    }

    // Driver's Code
    public static void main(String[] args)
    {
        int[] a = { 10, 5, 6, 2 };
        int[] b = { 12, 7, 9 };
        int N = a.length;
        int M = b.length;

        int[] merged = new int[M + N];

        // Function call
        mergeHeaps(merged, a, b, N, M);

        for (int i = 0; i < M + N; i++)
            System.out.print(merged[i] + " ");
        System.out.println();
    }
}

Python3

# Python3 program to merge two Max heaps.

# Standard heapify function to heapify a
# subtree rooted under idx. It assumes that
# subtrees of node are already heapified.


def MaxHeapify(arr, N, idx):

    # Find largest of node and
    # its children
    if idx >= N:
        return
    l = 2 * idx + 1
    r = 2 * idx + 2
    Max = 0
    if l < N and arr[l] > arr[idx]:
        Max = l
    else:
        Max = idx
    if r < N and arr[r] > arr[Max]:
        Max = r

    # Put Maximum value at root and
    # recur for the child with the
    # Maximum value
    if Max != idx:
        arr[Max], arr[idx] = arr[idx], arr[Max]
        MaxHeapify(arr, N, Max)

# Builds a Max heap of given arr[0..n-1]


def buildMaxHeap(arr, N):

    # building the heap from first non-leaf
    # node by calling Max heapify function
    for i in range(int(N / 2) - 1, -1, -1):
        MaxHeapify(arr, N, i)

# Merges Max heaps a[] and b[] into merged[]


def mergeHeaps(merged, a, b, N, M):

    # Copy elements of a[] and b[] one
    # by one to merged[]
    for i in range(N):
        merged[i] = a[i]
    for i in range(M):
        merged[N + i] = b[i]

    # build heap for the modified
    # array of size n+m
    buildMaxHeap(merged, N + M)


# Driver's code
if __name__ == '__main__':
    a = [10, 5, 6, 2]
    b = [12, 7, 9]

    N = len(a)
    M = len(b)

    merged = [0] * (M + N)

    # Function call
    mergeHeaps(merged, a, b, N, M)

    for i in range(N + M):
        print(merged[i], end=" ")

# This code is contributed by PranchalK

C#

// C# program to merge two max heaps.
using System;

class GfG {

    // Standard heapify function to heapify a
    // subtree rooted under idx. It assumes
    // that subtrees of node are already heapified.
    public static void maxHeapify(int[] arr, int N, int i)
    {
        // Find largest of node
        // and its children
        if (i >= N) {
            return;
        }
        int l = i * 2 + 1;
        int r = i * 2 + 2;
        int max;
        if (l < N && arr[l] > arr[i]) {
            max = l;
        }
        else
            max = i;
        if (r < N && arr[r] > arr[max]) {
            max = r;
        }

        // Put maximum value at root and
        // recur for the child with the
        // maximum value
        if (max != i) {
            int temp = arr[max];
            arr[max] = arr[i];
            arr[i] = temp;
            maxHeapify(arr, N, max);
        }
    }

    // Merges max heaps a[] and b[] into merged[]
    public static void mergeHeaps(int[] arr, int[] a,
                                  int[] b, int N, int M)
    {
        for (int i = 0; i < N; i++) {
            arr[i] = a[i];
        }
        for (int i = 0; i < M; i++) {
            arr[n + i] = b[i];
        }
        N = N + M;

        // Builds a max heap of given arr[0..n-1]
        for (int i = N / 2 - 1; i >= 0; i--) {
            maxHeapify(arr, N, i);
        }
    }

    // Driver Code
    public static void Main()
    {
        int[] a = { 10, 5, 6, 2 };
        int[] b = { 12, 7, 9 };
        int N = a.Length;
        int M = b.Length;

        int[] merged = new int[M + N];

        mergeHeaps(merged, a, b, N, M);

        for (int i = 0; i < M + N; i++)
            Console.Write(merged[i] + " ");
        Console.WriteLine();
    }
}
// This code is contributed by nitin mittal

Javascript

// javascript program to merge two max heaps.


    // Standard heapify function to heapify a
    // subtree rooted under idx. It assumes
    // that subtrees of node are already heapified.
    function maxHeapify(arr , n , i)
    {

        // Find largest of node and its children
        if (i >= n) {
            return;
        }
        var l = i * 2 + 1;
        var r = i * 2 + 2;
        var max;
        if (l < n && arr[l] > arr[i]) {
            max = l;
        } else
            max = i;
        if (r < n && arr[r] > arr[max]) {
            max = r;
        }

        // Put maximum value at root and
        // recur for the child with the
        // maximum value
        if (max != i) {
            var temp = arr[max];
            arr[max] = arr[i];
            arr[i] = temp;
            maxHeapify(arr, n, max);
        }
    }

    // Merges max heaps a and b into merged
    function mergeHeaps(arr,  a,  b , n , m) {
        for (var i = 0; i < n; i++) {
            arr[i] = a[i];
        }
        for (var i = 0; i < m; i++) {
            arr[n + i] = b[i];
        }
        n = n + m;

        // Builds a max heap of given arr[0..n-1]
        for (var i = parseInt(n / 2 - 1); i >= 0; i--) {
            maxHeapify(arr, n, i);
        }
    }

    // Driver Code
        var a = [ 10, 5, 6, 2 ];
        var b = [ 12, 7, 9 ];
        var n = a.length;
        var m = b.length;

        var merged = Array(m + n).fill(0);

        mergeHeaps(merged, a, b, n, m);

        for (var i = 0; i < m + n; i++)
            document.write(merged[i] + " ");

// This code is contributed by umadevi9616

PHP

<?php

function maxHeapify(&$arr, $N, $i)
{
    $largest = $i; // Initialize largest as root
    $l = 2*$i + 1; // left = 2*i + 1
    $r = 2*$i + 2; // right = 2*i + 2

    // If left child is larger than root
    if ($l < $N && $arr[$l] > $arr[$largest])
        $largest = $l;

    // If right child is larger than largest so far
    if ($r < $N && $arr[$r] > $arr[$largest])
        $largest = $r;

    // If largest is not root
    if ($largest != $i)
    {
        $swap = $arr[$i];
        $arr[$i] = $arr[$largest];
        $arr[$largest] = $swap;

        // Recursively heapify the affected sub-tree
        maxHeapify($arr, $N, $largest);
    }
}

function BuildMaxHeap(&$arr, $N)
{
      for ($i = ($N / 2) - 1; $i >= 0; $i--)
        maxHeapify($arr, $N, $i);
}

    // Driver's code
    $arrA = array(10, 5, 6, 2);
    $arrB = array(12, 7, 9);
      $N = sizeof($arrA)/sizeof($arrA[0]);
    $M = sizeof($arrB)/sizeof($arrB[0]);

    $mergedArray = array();

    // Push all the elements of array
    // arrA and arrB in mergedArray
    for($i = 0; $i < $N; $i++)
    array_push($mergedArray, $arrA[$i]);

      for($i = 0; $i < $M; $i++)
    array_push($mergedArray, $arrB[$i]);

    // Function call
      BuildMaxHeap($mergedArray, $N + $M);

      for ($i = 0; $i < $N + $M; ++$i)
           echo ($mergedArray[$i]." ");
?>

Output

12 10 9 2 5 7 6 

Time Complexity: O(N + M)
Auxiliary Space: O(N + M)  

Another Optimised Approach- Time Complexity: O(N + M) & Auxiliary Space: O(1)

Approach:

1. Initialize two indices, `i` and `j`, to track the current elements of arrays `a` and `b` respectively.

2. Use two boolean variables, `vis_next1` and `vis_next2`, to keep track of whether the next element of array `a` or `b` has been visited or not.

3. Iterate until either array `a` or array `b` is exhausted.

4. Compare current and the next elements of arrays `a` and `b` and select the maximum element among them.

5. Print the maximum element and update the indices and boolean variables accordingly.

6. If all elements of array `a` are processed, print the remaining elements of array `b`, and vice versa.

Below is the implementation of the above approach:

C++

#include <iostream>
using namespace std;

void mergeHeaps(int a[], int b[], int n, int m) {
    // vis_next1 & vis_next2 tells us next element of array "a"
  // and array "b" is visited or not respectively.
    bool vis_next1 = false, vis_next2 = false;
    // i & j is current index of array "a" and "b" respectively.
    int i = 0, j = 0;

    // Loop until end of array "a" or "b"
    while (i != n && j != m) {
        int max1 = i, max2 = j;

        // Check if next element of array "a" is greater than
      // current element
        if (i + 1 != n && !vis_next1 && a[i + 1] > a[i])
            max1 = i + 1;

        // Check if next element of array "b" is greater than
      // current element
        if (j + 1 != m && !vis_next2 && b[j + 1] > b[j])
            max2 = j + 1;

        // Compare the maximum elements from both arrays
        if (a[max1] > b[max2]) {
            cout << a[max1] << " ";

            // Update index and vis_next1 for array "a"
            if (max1 == i + 1)
                vis_next1 = true;
            else {
                if (vis_next1) {
                    i += 2;
                    vis_next1 = false;
                }
                else
                    i++;
            }
        }
        else {
            cout << b[max2] << " ";

            // Update index and vis_next2 for array "b"
            if (max2 == j + 1)
                vis_next2 = true;
            else {
                if (vis_next2) {
                    j += 2;
                    vis_next2 = false;
                }
                else
                    j++;
            }
        }
    }

    // Print remaining elements of array "b" if array "a" is
  // exhausted
    if (i == n) {
        while (j != m) {
            cout << b[j] << " ";
            j++;
            if (vis_next2) {
                vis_next2 = false;
                j++;
            }
        }
    }
    // Print remaining elements of array "a" if array "b" is
  // exhausted
    else {
        while (i != n) {
            cout << a[i] << " ";
            i++;
            if (vis_next1) {
                vis_next1 = false;
                i++;
            }
        }
    }
    return;
}

// Driver's code
int main() {
    int a[] = { 10, 5, 6, 2 };
    int b[] = { 12, 7, 9 };

    int N = sizeof(a) / sizeof(a[0]);
    int M = sizeof(b) / sizeof(b[0]);

    // Function call
    mergeHeaps(a, b, N, M);

    return 0;
}

Java

import java.io.*;

class GFG {
  static void mergeHeaps(int a[], int b[], int n, int m) {
    // vis_next1 & vis_next2 tells us next element of array "a"
    // and array "b" is visited or not respectively.
    boolean vis_next1 = false, vis_next2 = false;
    // i & j is current index of array "a" and "b" respectively.
    int i = 0, j = 0;

    // Loop until end of array "a" or "b"
    while (i != n && j != m) {
        int max1 = i, max2 = j;

        // Check if next element of array "a" is greater than
      // current element
        if (i + 1 != n && !vis_next1 && a[i + 1] > a[i])
            max1 = i + 1;

        // Check if next element of array "b" is greater than
      // current element
        if (j + 1 != m && !vis_next2 && b[j + 1] > b[j])
            max2 = j + 1;

        // Compare the maximum elements from both arrays
        if (a[max1] > b[max2]) {
            System.out.print(a[max1]+" ");

            // Update index and vis_next1 for array "a"
            if (max1 == i + 1)
                vis_next1 = true;
            else {
                if (vis_next1) {
                    i += 2;
                    vis_next1 = false;
                }
                else
                    i++;
            }
        }
        else {
            System.out.print(b[max2]+" ");

            // Update index and vis_next2 for array "b"
            if (max2 == j + 1)
                vis_next2 = true;
            else {
                if (vis_next2) {
                    j += 2;
                    vis_next2 = false;
                }
                else
                    j++;
            }
        }
    }

    // Print remaining elements of array "b" if array "a" is exhausted
    if (i == n) {
        while (j != m) {
            System.out.print(b[j]+" ");
            j++;
            if (vis_next2) {
                vis_next2 = false;
                j++;
            }
        }
    }
    // Print remaining elements of array "a" if array "b"
    // is exhausted
    else {
        while (i != n) {
            System.out.print(a[i]+" ");
            i++;
            if (vis_next1) {
                vis_next1 = false;
                i++;
            }
        }
    }
    return;
}
public static void main (String[] args) {
    int a[] = { 10, 5, 6, 2 };
    int b[] = { 12, 7, 9 };

    int N = a.length;
    int M = b.length;

    // Function call
    mergeHeaps(a, b, N, M);

   }
}
//this code contributed by shubhamrajput6156

Python3

def mergeHeaps(a, b, n, m):
    # vis_next1 & vis_next2 tells us if the next element of array "a"
    # and array "b" is visited or not, respectively.
    vis_next1 = False
    vis_next2 = False
    # i & j are the current indices of arrays "a" and "b", respectively.
    i = 0
    j = 0

    # Loop until the end of array "a" or "b"
    while i != n and j != m:
        max1 = i
        max2 = j

        # Check if the next element of array "a" is greater than
        # the current element
        if i + 1 != n and not vis_next1 and a[i + 1] > a[i]:
            max1 = i + 1

        # Check if the next element of array "b" is greater than
        # the current element
        if j + 1 != m and not vis_next2 and b[j + 1] > b[j]:
            max2 = j + 1

        # Compare the maximum elements from both arrays
        if a[max1] > b[max2]:
            print(a[max1], end=" ")

            # Update index and vis_next1 for array "a"
            if max1 == i + 1:
                vis_next1 = True
            else:
                if vis_next1:
                    i += 2
                    vis_next1 = False
                else:
                    i += 1
        else:
            print(b[max2], end=" ")

            # Update index and vis_next2 for array "b"
            if max2 == j + 1:
                vis_next2 = True
            else:
                if vis_next2:
                    j += 2
                    vis_next2 = False
                else:
                    j += 1

    # Print remaining elements of array "b" if array "a" is exhausted
    if i == n:
        while j != m:
            print(b[j], end=" ")
            j += 1
            if vis_next2:
                vis_next2 = False
                j += 1
    # Print remaining elements of array "a" if array "b" is exhausted
    else:
        while i != n:
            print(a[i], end=" ")
            i += 1
            if vis_next1:
                vis_next1 = False
                i += 1

# Driver's code
if __name__ == "__main__":
    a = [10, 5, 6, 2]
    b = [12, 7, 9]
    N = len(a)
    M = len(b)

    # Function call
    mergeHeaps(a, b, N, M)

# This code is contributed by shivamgupta310570

C#

using System;

class Program
{
    static void MergeHeaps(int[] a, int[] b, int n, int m)
    {
        bool visNext1 = false; // Tracks if the next element of array "a" is visited
        bool visNext2 = false; // Tracks if the next element of array "b" is visited
        int i = 0; // Current index for array "a"
        int j = 0; // Current index for array "b"

        while (i != n && j != m)
        {
            int max1 = i;
            int max2 = j;

            // Check if the next element of array "a" is greater than the current element
            if (i + 1 != n && !visNext1 && a[i + 1] > a[i])
                max1 = i + 1;

            // Check if the next element of array "b" is greater than the current element
            if (j + 1 != m && !visNext2 && b[j + 1] > b[j])
                max2 = j + 1;

            if (a[max1] > b[max2])
            {
                Console.Write(a[max1] + " "); // Print the greater element from array "a"

                if (max1 == i + 1)
                    visNext1 = true;
                else
                {
                    if (visNext1)
                    {
                        i += 2;
                        visNext1 = false;
                    }
                    else
                        i++;
                }
            }
            else
            {
                Console.Write(b[max2] + " "); // Print the greater element from array "b"

                if (max2 == j + 1)
                    visNext2 = true;
                else
                {
                    if (visNext2)
                    {
                        j += 2;
                        visNext2 = false;
                    }
                    else
                        j++;
                }
            }
        }

        if (i == n)
        {
            // Print the remaining elements of array "b" if array "a" is exhausted
            while (j != m)
            {
                Console.Write(b[j] + " ");
                j++;
                if (visNext2)
                {
                    visNext2 = false;
                    j++;
                }
            }
        }
        else
        {
            // Print the remaining elements of array "a" if array "b" is exhausted
            while (i != n)
            {
                Console.Write(a[i] + " ");
                i++;
                if (visNext1)
                {
                    visNext1 = false;
                    i++;
                }
            }
        }
    }

    static void Main()
    {
        int[] a = { 10, 5, 6, 2 };
        int[] b = { 12, 7, 9 };

        int n = a.Length;
        int m = b.Length;

        MergeHeaps(a, b, n, m);
    }
}

Javascript

function mergeHeaps(a, b, n, m) {
    // vis_next1 & vis_next2 tells us next element of array "a"
    // and array "b" is visited or not respectively.
    let vis_next1 = false;
    let vis_next2 = false;
    // i & j is current index of array "a" and "b" respectively
    let i = 0;
    let j = 0;

    // Loop until end of array "a" or "b"
    while (i !== n && j !== m) {
        let max1 = i;
        let max2 = j;

        // Check if next element of array "a" is greater than
        // current element
        if (i + 1 !== n && !vis_next1 && a[i + 1] > a[i])
            max1 = i + 1;

        // Check if next element of array "b" is greater than
        // current element
        if (j + 1 !== m && !vis_next2 && b[j + 1] > b[j])
            max2 = j + 1;

        // Compare the maximum elements from both arrays
        if (a[max1] > b[max2]) {
            console.log(a[max1] + " ");

            // Update index and vis_next1 for array "a"
            if (max1 === i + 1)
                vis_next1 = true;
            else {
                if (vis_next1) {
                    i += 2;
                    vis_next1 = false;
                }
                else
                    i++;
            }
        }
        else {
            console.log(b[max2] + " ");

            // Update index and vis_next2 for array "b"
            if (max2 === j + 1)
                vis_next2 = true;
            else {
                if (vis_next2) {
                    j += 2;
                    vis_next2 = false;
                }
                else
                    j++;
            }
        }
    }

    // Print remaining elements of array "b" if array "a" is
    // exhausted
    if (i === n) {
        while (j !== m) {
            console.log(b[j] + " ");
            j++;
            if (vis_next2) {
                vis_next2 = false;
                j++;
            }
        }
    }
    // Print remaining elements of array "a" if array "b" is
    // exhausted
    else {
        while (i !== n) {
            console.log(a[i] + " ");
            i++;
            if (vis_next1) {
                vis_next1 = false;
                i++;
            }
        }
    }
}

// Driver's code
const a = [10, 5, 6, 2];
const b = [12, 7, 9];
const N = a.length;
const M = b.length;

// Function call
mergeHeaps(a, b, N, M);

Output

12 10 9 7 5 6 2 

Time Complexity: O(N + M)
Auxiliary Space: O(1)