Maximum litres of water that can be bought with N Rupees
Last Updated :
29 Sep, 2022
Given 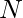 Rupees. A liter plastic bottle of water costs
Rupees. A liter plastic bottle of water costs 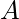 Rupees and a litre of glass bottle of water costs
Rupees and a litre of glass bottle of water costs 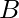 Rupees. But the empty glass bottle after buying can be exchanged for
Rupees. But the empty glass bottle after buying can be exchanged for 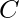 Rupees. Find the maximum liters of water which can be bought with
Rupees. Find the maximum liters of water which can be bought with 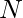 Rupees.
Rupees.
Examples:
Input: N = 10 , A = 11 , B = 9 , C = 8
Output: 2
One glass bottle can be bought and then can be returned to buy one more glass bottle
Input: N = 15 , A = 6 , B = 4 , C = 3
Output: 12
Approach: If we have at least 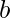 money then cost of one glass bottle is b – c. This means that if a ? (b – c) then we don’t need to buy glass bottles, only plastic ones, and the answer will be floor(n / a). Otherwise we need to buy glass bottles while we can.
money then cost of one glass bottle is b – c. This means that if a ? (b – c) then we don’t need to buy glass bottles, only plastic ones, and the answer will be floor(n / a). Otherwise we need to buy glass bottles while we can.
So, if we have at least 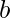 money, then we will buy floor((n – c) / (b – c)) glass bottles and then spend rest of the money on plastic ones.
money, then we will buy floor((n – c) / (b – c)) glass bottles and then spend rest of the money on plastic ones.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
void maxLitres(int budget,int plastic,int glass,int refund)
{
if (glass - refund < plastic)
{
int ans = max((budget - refund) / (glass - refund), 0);
budget -= ans * (glass - refund);
ans += budget / plastic;
cout<<ans<<endl;
}
else
cout<<(budget / plastic)<<endl;
}
int main()
{
int budget = 10, plastic=11, glass=9, refund = 8;
maxLitres(budget, plastic, glass, refund);
}
|
Java
class GFG
{
static void maxLitres(int budget, int plastic,
int glass, int refund)
{
if (glass - refund < plastic)
{
int ans = Math.max((budget - refund) / (glass - refund), 0);
budget -= ans * (glass - refund);
ans += budget / plastic;
System.out.println(ans);
}
else
{
System.out.println((budget / plastic));
}
}
public static void main(String[] args)
{
int budget = 10, plastic = 11, glass = 9, refund = 8;
maxLitres(budget, plastic, glass, refund);
}
}
|
Python3
def maxLitres(budget, plastic, glass, refund):
if glass - refund < plastic:
ans = max((budget - refund) // (glass - refund), 0)
budget -= ans * (glass - refund)
ans += budget // plastic
print(ans)
else:
print(budget // plastic)
budget, plastic, glass, refund = 10, 11, 9, 8
maxLitres(budget, plastic, glass, refund)
|
C#
using System;
class GFG
{
static void maxLitres(int budget, int plastic,
int glass, int refund)
{
if (glass - refund < plastic)
{
int ans = Math.Max((budget - refund) / (glass - refund), 0);
budget -= ans * (glass - refund);
ans += budget / plastic;
Console.WriteLine(ans);
}
else
{
Console.WriteLine((budget / plastic));
}
}
public static void Main(String[] args)
{
int budget = 10, plastic = 11, glass = 9, refund = 8;
maxLitres(budget, plastic, glass, refund);
}
}
|
PHP
<?php
function maxLitres($budget, $plastic,
$glass, $refund)
{
if ($glass - $refund < $plastic)
{
$ans = max((int)($budget - $refund) /
($glass - $refund), 0);
$budget -= $ans * ($glass - $refund);
$ans += (int)($budget / $plastic);
echo $ans . "\n";
}
else
echo (int)($budget / $plastic) . "\n";
}
$budget = 10;
$plastic = 11;
$glass = 9;
$refund = 8;
maxLitres($budget, $plastic,
$glass, $refund);
?>
|
Javascript
<script>
function maxLitres(budget, plastic,
glass, refund)
{
if (glass - refund < plastic)
{
let ans = Math.max((budget - refund) / (glass - refund), 0);
budget -= ans * (glass - refund);
ans += Math.floor(budget / plastic);
document.write(ans);
}
else
{
document.write(Math.floor(budget / plastic));
}
}
let budget = 10, plastic = 11, glass = 9, refund = 8;
maxLitres(budget, plastic, glass, refund);
</script>
|
Time complexity: O(1)
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...