Maximize minimum array element possible by exactly K decrements

Given an array arr[] consisting of N integers and an integer K, the task is to maximize the minimum element of the array after decrementing array elements exactly K number of times.

Examples:

Input: arr[] = {2, 4, 4}, K = 3 
Output: 2
Explanation:
One of the possible way is:

1. Decrement arr[2] by 1. The array modifies to {2, 4, 3}.
2. Decrement arr[1] by 1. The array modifies to {2, 3, 3}.
3. Decrement arr[2] by 1. The array modifies to {2, 3, 2}.

Therefore, the minimum array element that can be obtained is 2, which it is the maximum possible value.

Input: arr[] = {10, 10, 10, 10, 10}, K = 10 
Output: 8

Naive Approach: The simplest approach to solve the given problem is to iterate over the range [1, K] and in each iteration, find the maximum element of the array and then decrement it by 1. After the above steps then print the minimum element of the array.

Time Complexity: O(N * K)
Auxiliary Space: O(1)

Efficient Approach: The above problem can also be optimized based on the following observations: 

• It can be observed that the optimal way is to first decrement all the values of the array to the minimum element of the array.
• The total moves needed to make all the elements equal to the min-element is the sum of the array decremented by K times the minimum element of the array.
• If the total number of moves needed to make all the elements equal to the minimum element is less than K then the minimum element will be the answer.
• Otherwise, it will be optimal to decrement from each element of the array by 1 until K becomes 0. Then minimum element will be equal to .

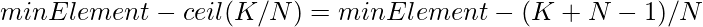Follow the steps to solve the problem:

• Find the minimum element of the array arr[] and store it in a variable say minElement.
• Initialize a variable, say reqOperation as 0 to store the total number of moves needed to make all the elements equal to the minElement of the array.
• Traverse the array arr[] and in each iteration, increment reqOperation by the current element of the array subtracted by the minElement.
• If reqOperation is greater than K then print minElement. Otherwise, print the value of minElement – (K + N – 1) / N as the resultant minimum element.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the maximized
// minimum element of the array
// after performing given operation
// exactly K times
int minimumElement(int arr[], int N,
                   int K)
{
    // Stores the minimum element
    int minElement = arr[0];

    // Traverse the given array
    for (int i = 0; i < N; ++i) {

        // Update the minimum element
        minElement = min(minElement,
                         arr[i]);
    }

    // Stores the required operations
    // to make all elements equal to
    // the minimum element
    int reqOperations = 0;

    for (int i = 0; i < N; ++i) {

        // Update required operations
        reqOperations += arr[i] - minElement;
    }

    // If reqOperations < K
    if (reqOperations < K) {

        // Decrement the value of K
        // by reqOperations
        K -= reqOperations;

        // Update minElement
        minElement -= (K + N - 1) / N;
    }

    // Return minimum element
    return minElement;
}

// Driver Code
int main()
{

    int arr[] = { 10, 10, 10, 10 };
    int K = 7;
    int N = sizeof(arr) / sizeof(arr[0]);
    cout << minimumElement(arr, N, K);

    return 0;
}

Java

// Java program for the above approach
import java.io.*;
class GFG
{

    // Function to find the maximized
    // minimum element of the array
    // after performing given operation
    // exactly K times
    static int minimumElement(int arr[], int N, int K)
    {

        // Stores the minimum element
        int minElement = arr[0];

        // Traverse the given array
        for (int i = 0; i < N; ++i) {

            // Update the minimum element
            minElement = Math.min(minElement, arr[i]);
        }

        // Stores the required operations
        // to make all elements equal to
        // the minimum element
        int reqOperations = 0;

        for (int i = 0; i < N; ++i) {

            // Update required operations
            reqOperations += arr[i] - minElement;
        }

        // If reqOperations < K
        if (reqOperations < K) {

            // Decrement the value of K
            // by reqOperations
            K -= reqOperations;

            // Update minElement
            minElement -= (K + N - 1) / N;
        }

        // Return minimum element
        return minElement;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int arr[] = { 10, 10, 10, 10 };
        int K = 7;
        int N = arr.length;
        System.out.println(minimumElement(arr, N, K));

    }
}

        // This code is contributed by Potta Lokesh

Python3

# Python program for the above approach

# Function to find the maximized
# minimum element of the array
# after performing given operation
# exactly K times
def minimumElement(arr, N, K):

    # Stores the minimum element
    minElement = arr[0];

    # Traverse the given array
    for i in range(N):

        # Update the minimum element
        minElement = min(minElement, arr[i]);

    # Stores the required operations
    # to make all elements equal to
    # the minimum element
    reqOperations = 0;

    for i in range(N):

        # Update required operations
        reqOperations += arr[i] - minElement

    # If reqOperations < K
    if (reqOperations < K):

        # Decrement the value of K
        # by reqOperations
        K -= reqOperations;

        # Update minElement
        minElement -= (K + N - 1) // N;

    # Return minimum element
    return minElement;


# Driver Code
arr = [ 10, 10, 10, 10 ];
K = 7;
N = len(arr)

print(minimumElement(arr, N, K));

# This code is contributed by _saurabh_jaiswal

C#

// C# program for the above approach
using System;
class GFG
{

    // Function to find the maximized
    // minimum element of the array
    // after performing given operation
    // exactly K times
    static int minimumElement(int []arr, int N, int K)
    {

        // Stores the minimum element
        int minElement = arr[0];

        // Traverse the given array
        for (int i = 0; i < N; ++i) {

            // Update the minimum element
            minElement = Math.Min(minElement, arr[i]);
        }

        // Stores the required operations
        // to make all elements equal to
        // the minimum element
        int reqOperations = 0;

        for (int i = 0; i < N; ++i) {

            // Update required operations
            reqOperations += arr[i] - minElement;
        }

        // If reqOperations < K
        if (reqOperations < K) {

            // Decrement the value of K
            // by reqOperations
            K -= reqOperations;

            // Update minElement
            minElement -= (K + N - 1) / N;
        }

        // Return minimum element
        return minElement;
    }

    // Driver Code
    public static void Main(string[] args)
    {
        int[] arr= { 10, 10, 10, 10 };
        int K = 7;
        int N = arr.Length;
        Console.Write(minimumElement(arr, N, K));

    }
}

// This code is contributed by ukasp.

Javascript

<script>

// Javascript program for the above approach

// Function to find the maximized
// minimum element of the array
// after performing given operation
// exactly K times
function minimumElement(arr, N, K)
{

    // Stores the minimum element
    let minElement = arr[0];

    // Traverse the given array
    for(let i = 0; i < N; ++i)
    {

        // Update the minimum element
        minElement = Math.min(minElement,
            arr[i]);
    }

    // Stores the required operations
    // to make all elements equal to
    // the minimum element
    let reqOperations = 0;

    for(let i = 0; i < N; ++i)
    {

        // Update required operations
        reqOperations += arr[i] - minElement;
    }

    // If reqOperations < K
    if (reqOperations < K)
    {

        // Decrement the value of K
        // by reqOperations
        K -= reqOperations;

        // Update minElement
        minElement -= Math.floor((K + N - 1) / N);
    }

    // Return minimum element
    return minElement;
}

// Driver Code
let arr = [ 10, 10, 10, 10 ];
let K = 7;
let N = arr.length;

document.write(minimumElement(arr, N, K));

// This code is contributed by _saurabh_jaiswal

</script>

Output:

8

Time Complexity: O(N)
Auxiliary Space: O(1)