In-Place Algorithm

In-place has more than one definition. One strict definition is. 

An in-place algorithm is an algorithm that does not need an extra space and produces an output in the same memory that contains the data by transforming the input ‘in-place’. However, a small constant extra space used for variables is allowed.

A more broad definition is,  

In-place means that the algorithm does not use extra space for manipulating the input but may require a small though non-constant extra space for its operation. Usually, this space is O(log n), though sometimes anything in O(n) (Smaller than linear) is allowed.

A Not In-Place Implementation of reversing an array 

Implementation:

C++

// An Not in-place C++ program to reverse an array
#include <bits/stdc++.h>
using namespace std;

/* Function to reverse arr[] from start to end*/
void reverseArray(int arr[], int n)
{
   // Create a copy array and store reversed
   // elements
   int rev[n];
   for (int i=0; i<n; i++)
       rev[n-i-1] = arr[i];

   // Now copy reversed elements back to arr[]
   for (int i=0; i<n; i++)
       arr[i] = rev[i];
}

/* Utility function to print an array */
void printArray(int arr[], int size)
{
   for (int i = 0; i < size; i++)
      cout << arr[i] << " ";
   cout << endl;
}

/* Driver function to test above functions */
int main()
{
    int arr[] = {1, 2, 3, 4, 5, 6};
    int n = sizeof(arr)/sizeof(arr[0]);
    printArray(arr, n);
    reverseArray(arr, n);
    cout << "Reversed array is" << endl;
    printArray(arr, n);
    return 0;
}

Java

// An Not in-place Java program
// to reverse an array
import java.util.*;

class GFG
{
    /* Function to reverse arr[]
       from start to end*/
    public static void reverseArray(int []arr,
                                     int n)
    {
        // Create a copy array
        // and store reversed
        // elements
        int []rev = new int[n];
        for (int i = 0; i < n; i++)
            rev[n - i - 1] = arr[i];

        // Now copy reversed
        // elements back to arr[]
        for (int i = 0; i < n; i++)
            arr[i] = rev[i];
    }

    /* Utility function to
       print an array */
    public static void printArray(int []arr,
                                  int size)
    {
    for (int i = 0; i < size; i++)
        System.out.print(arr[i] + " ");
    System.out.println("");
    }

    // Driver code
    public static void main(String[] args)
    {
        int arr[] = {1, 2, 3, 4, 5, 6};
        int n = arr.length;
        printArray(arr, n);
        reverseArray(arr, n);
        System.out.println("Reversed array is");
        printArray(arr, n);
    }
}

// This code is contributed
// by Harshit Saini

Python3

# An Not in-place Python program
# to reverse an array

''' Function to reverse arr[]
    from start to end '''
def reverseArray(arr, n):

    # Create a copy array
    # and store reversed
    # elements
    rev = n * [0]
    for i in range(0, n):
        rev[n - i - 1] = arr[i]

    # Now copy reversed
    # elements back to arr[]
    for i in range(0, n):
        arr[i] = rev[i]

# Driver code
if __name__ == "__main__":
    arr = [1, 2, 3, 4, 5, 6]
    n = len(arr)
    print(*arr)
    reverseArray(arr, n);
    print("Reversed array is")
    print(*arr)

# This code is contributed
# by Harshit Saini

C#

// An Not in-place C# program
// to reverse an array
using System;

class GFG
{
    /* Function to reverse arr[]
    from start to end*/
    public static void reverseArray(int[] arr,
                                    int n)
    {
        // Create a copy array
        // and store reversed
        // elements
        int[] rev = new int[n];
        for (int i = 0; i < n; i++)
            rev[n - i - 1] = arr[i];

        // Now copy reversed
        // elements back to arr[]
        for (int i = 0; i < n; i++)
            arr[i] = rev[i];
    }

    /* Utility function to
    print an array */
    public static void printArray(int[] arr,
                                int size)
    {
    for (int i = 0; i < size; i++)
        Console.Write(arr[i] + " ");
    Console.Write("\n");
    }

    // Driver code
    public static void Main()
    {
        int[] arr = {1, 2, 3, 4, 5, 6};
        int n = arr.Length;
        printArray(arr, n);
        reverseArray(arr, n);
        Console.WriteLine("Reversed array is");
        printArray(arr, n);
    }
}

// This code is contributed by Ita_c.

Javascript

<script>
// An Not in-place Javascript program
// to reverse an array

    /* Function to reverse arr[]
       from start to end*/
    function reverseArray(arr,n)
    {
        // Create a copy array
        // and store reversed
        // elements
        let rev = new Array(n);
        for (let i = 0; i < n; i++)
            rev[n - i - 1] = arr[i];

        // Now copy reversed
        // elements back to arr[]
        for (let i = 0; i < n; i++)
            arr[i] = rev[i];
    }

    /* Utility function to
       print an array */
    function printArray(arr,size)
    {
        for (let i = 0; i < size; i++)
            document.write(arr[i] + " ");
        document.write("<br>");
    }

    // Driver code
    let arr=[1, 2, 3, 4, 5, 6];
    let n = arr.length;
    printArray(arr, n);
    reverseArray(arr, n);
    document.write("Reversed array is<br>");
    printArray(arr, n);


    // This code is contributed by rag2127
</script>

Output

1 2 3 4 5 6 
Reversed array is
6 5 4 3 2 1 

Time Complexity: O(n)

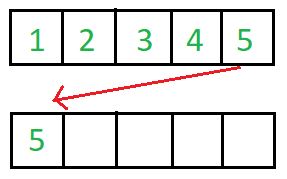
This needs O(n) extra space and is an example of a not-in-place algorithm.

An In-Place Implementation of Reversing an array. 

Implementation:

C++

// An in-place C++ program to reverse an array
#include <bits/stdc++.h>
using namespace std;

/* Function to reverse arr[] from start to end*/
void reverseArray(int arr[], int n)
{
   for (int i=0; i<n/2; i++)
     swap(arr[i], arr[n-i-1]);
}

/* Utility function to print an array */
void printArray(int arr[], int size)
{
   for (int i = 0; i < size; i++)
      cout << arr[i] << " ";
   cout << endl;
}

/* Driver function to test above functions */
int main()
{
    int arr[] = {1, 2, 3, 4, 5, 6};
    int n = sizeof(arr)/sizeof(arr[0]);
    printArray(arr, n);
    reverseArray(arr, n);
    cout << "Reversed array is" << endl;
    printArray(arr, n);
    return 0;
}

Java

// An in-place Java program
// to reverse an array
import java.util.*;

class GFG
{
    public static int __(int x, int y) {return x;}

    /* Function to reverse arr[]
       from start to end*/
    public static void reverseArray(int []arr,
                                     int n)
    {
        for (int i = 0; i < n / 2; i++)
            arr[i] = __(arr[n - i - 1],
                        arr[n - i - 1] = arr[i]);
    }

    /* Utility function to
       print an array */
    public static void printArray(int []arr,
                                  int size)
    {
        for (int i = 0; i < size; i++)
            System.out.print(Integer.toString(arr[i]) + " ");
        System.out.println("");
    }

    // Driver code
    public static void main(String[] args)
    {
        int []arr = new int[]{1, 2, 3, 4, 5, 6};
        int n = arr.length;
        printArray(arr, n);
        reverseArray(arr, n);
        System.out.println("Reversed array is");
        printArray(arr, n);
    }
}

// This code is contributed
// by Harshit Saini

Python3

# An in-place Python program
# to reverse an array

''' Function to reverse arr[]
    from start to end'''
def reverseArray(arr, n):

    for i in range(0, int(n / 2)):
        arr[i], arr[n - i - 1] = arr[n - i - 1], arr[i]


# Driver code
if __name__ == "__main__":

    arr = [1, 2, 3, 4, 5, 6]
    n = len(arr)
    print(*arr)
    reverseArray(arr, n)
    print("Reversed array is")
    print(*arr)

# This code is contributed
# by Harshit Saini

C#

// An in-place C# program
// to reverse an array
using System;

class GFG
{
    public static int __(int x, int y) {return x;}

    /* Function to reverse arr[]
    from start to end*/
    public static void reverseArray(int []arr,
                                    int n)
    {
        for (int i = 0; i < n / 2; i++)
            arr[i] = __(arr[n - i - 1],
                        arr[n - i - 1] = arr[i]);
    }

    /* Utility function to
    print an array */
    public static void printArray(int []arr,
                                int size)
    {
        for (int i = 0; i < size; i++)
            Console.Write(arr[i] + " ");
        Console.WriteLine("");
    }

    // Driver code
    public static void Main(String[] args)
    {
        int []arr = new int[]{1, 2, 3, 4, 5, 6};
        int n = arr.Length;
        printArray(arr, n);
        reverseArray(arr, n);
        Console.WriteLine("Reversed array is");
        printArray(arr, n);
    }
}

/* This code is contributed by PrinciRaj1992 */

Javascript

<script>
// An in-place Javascript program
// to reverse an array

    function  __(x,y)
    {
        return x;
    }

    /* Function to reverse arr[]
       from start to end*/
    function reverseArray(arr,n)
    {
        for (let i = 0; i < n / 2; i++)
            arr[i] = __(arr[n - i - 1],
                        arr[n - i - 1] = arr[i]);
    }

    /* Utility function to
       print an array */
    function printArray(arr,size)
    {
        for (let i = 0; i < size; i++)
            document.write(arr[i] + " ");
        document.write("<br>");
    }

    // Driver code
    let arr=[1, 2, 3, 4, 5, 6];
    let n = arr.length;
    printArray(arr, n);
    reverseArray(arr, n);
    document.write("Reversed array is<br>");
    printArray(arr, n);


// This code is contributed by avanitrachhadiya2155
</script>

Output

1 2 3 4 5 6 
Reversed array is
6 5 4 3 2 1 

Time Complexity: O(n)

This needs O(1) extra space for exchanging elements and is an example of an in-place algorithm.

Which Sorting Algorithms are In-Place and which are not?
In Place: Bubble sort, Selection Sort, Insertion Sort, Heapsort.
Not In-Place: Merge Sort. Note that merge sort requires O(n) extra space.

What about QuickSort? Why is it called In-Place?
QuickSort uses extra space for recursive function calls. It is called in-place according to broad definition as extra space required is not used to manipulate input, but only for recursive calls.