MATLAB – Butterworth Highpass Filter in Image Processing
Last Updated :
10 May, 2020
In the field of Image Processing,
Butterworth Highpass Filter (BHPF) is used for image sharpening in the frequency domain. Image Sharpening is a technique to enhance the fine details and highlight the edges in a digital image. It removes low-frequency components from an image and preserves high-frequency components.
This Butterworth highpass filter is the reverse operation of the Butterworth lowpass filter. It can be determined using the relation-
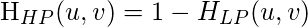
where,

is the transfer function of the highpass filter and
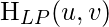
is the transfer function of the corresponding lowpass filter.
The transfer function of BHPF of order
is defined as-
![Rendered by QuickLaTeX.com H(u, v)=\frac{1}{1+\left[D_{0} / D(u, v)\right]^{2 n}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8900041cefd583b25d91c91cfea564ad_l3.png)
Where,
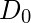 is a positive constant. BHPF passes all the frequencies greater than
is a positive constant. BHPF passes all the frequencies greater than 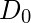 value without attenuation and cuts off all the frequencies less than it.
value without attenuation and cuts off all the frequencies less than it. - This
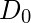 is the transition point between H(u, v) = 1 and H(u, v) = 0, so this is termed as cutoff frequency. But instead of making a sharp cut-off (like, Ideal Highpass Filter (IHPF)), it introduces a smooth transition from 0 to 1 to reduce ringing artifacts.
is the transition point between H(u, v) = 1 and H(u, v) = 0, so this is termed as cutoff frequency. But instead of making a sharp cut-off (like, Ideal Highpass Filter (IHPF)), it introduces a smooth transition from 0 to 1 to reduce ringing artifacts.
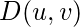 is the Euclidean Distance from any point (u, v) to the origin of the frequency plane, i.e,
is the Euclidean Distance from any point (u, v) to the origin of the frequency plane, i.e, 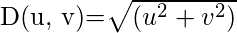
Approach:
Step 1: Input – Read an image
Step 2: Saving the size of the input image in pixels
Step 3: Get the Fourier Transform of the input_image
Step 4: Assign the order 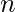 and cut-off frequency
and cut-off frequency 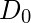 Step 5: Designing filter: Butterworth High Pass Filter
Step 6: Convolution between the Fourier Transformed input image and the filtering mask
Step 7: Take Inverse Fourier Transform of the convoluted image
Step 8: Display the resultant image as output
Step 5: Designing filter: Butterworth High Pass Filter
Step 6: Convolution between the Fourier Transformed input image and the filtering mask
Step 7: Take Inverse Fourier Transform of the convoluted image
Step 8: Display the resultant image as output
Implementation in MATLAB:
input_image = imread('[name of input image file].[file format]');
[M, N] = size(input_image);
FT_img = fft2(double(input_image));
n = 2;
D0 = 10;
u = 0:(M-1);
v = 0:(N-1);
idx = find(u > M/2);
u(idx) = u(idx) - M;
idy = find(v > N/2);
v(idy) = v(idy) - N;
[V, U] = meshgrid(v, u);
D = sqrt(U.^2 + V.^2);
H = 1./(1 + (D0./D).^(2*n));
G = H.*FT_img;
output_image = real(ifft2(double(G)));
subplot(2, 1, 1), imshow(input_image),
subplot(2, 1, 2), imshow(output_image, [ ]);
|
Input Image –
 Output:
Output:
 Note:
Note: The result of BHPF is much smoother than IHPF. Here, the boundaries are much less distorted, even for the smallest value of cutoff frequency. The transition into higher values of cutoff frequencies is much smoother with the BHPF.
Share your thoughts in the comments
Please Login to comment...