MATLAB – Butterworth Lowpass Filter in Image Processing
Last Updated :
10 May, 2020
In the field of Image Processing,
Butterworth Lowpass Filter (BLPF) is used for image smoothing in the frequency domain. It removes high-frequency noise from a digital image and preserves low-frequency components. The transfer function of BLPF of order
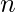
is defined as-
![Rendered by QuickLaTeX.com H(u, v)=\frac{1}{1+\left[D(u, v) / D_{0}\right]^{2 n}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fcafcde59c5df351d4fae6e8be1f4773_l3.png)
Where,
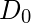 is a positive constant. BLPF passes all the frequencies less than
is a positive constant. BLPF passes all the frequencies less than 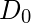 value without attenuation and cuts off all the frequencies greater than it.
value without attenuation and cuts off all the frequencies greater than it. - This
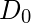 is the transition point between H(u, v) = 1 and H(u, v) = 0, so this is termed as cutoff frequency. But instead of making a sharp cut-off (like, Ideal Lowpass Filter (ILPF)), it introduces a smooth transition from 1 to 0 to reduce ringing artifacts.
is the transition point between H(u, v) = 1 and H(u, v) = 0, so this is termed as cutoff frequency. But instead of making a sharp cut-off (like, Ideal Lowpass Filter (ILPF)), it introduces a smooth transition from 1 to 0 to reduce ringing artifacts.
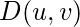 is the Euclidean Distance from any point (u, v) to the origin of the frequency plane, i.e,
is the Euclidean Distance from any point (u, v) to the origin of the frequency plane, i.e, 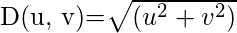
Approach:
Step 1: Input – Read an image
Step 2: Saving the size of the input image in pixels
Step 3: Get the Fourier Transform of the input_image
Step 4: Assign the order  and cut-off frequency
and cut-off frequency  Step 5: Designing filter: Butterworth Low Pass Filter
Step 6: Convolution between the Fourier Transformed input image and the filtering mask
Step 7: Take Inverse Fourier Transform of the convoluted image
Step 8: Display the resultant image as output
Step 5: Designing filter: Butterworth Low Pass Filter
Step 6: Convolution between the Fourier Transformed input image and the filtering mask
Step 7: Take Inverse Fourier Transform of the convoluted image
Step 8: Display the resultant image as output
Implementation in MATLAB:
input_image = imread('[name of input image file].[file format]');
[M, N] = size(input_image);
FT_img = fft2(double(input_image));
n = 2;
D0 = 20;
u = 0:(M-1);
v = 0:(N-1);
idx = find(u > M/2);
u(idx) = u(idx) - M;
idy = find(v > N/2);
v(idy) = v(idy) - N;
[V, U] = meshgrid(v, u);
D = sqrt(U.^2 + V.^2);
H = 1./(1 + (D./D0).^(2*n));
G = H.*FT_img;
output_image = real(ifft2(double(G)));
subplot(2, 1, 1), imshow(input_image),
subplot(2, 1, 2), imshow(output_image, [ ]);
|
Input Image –
 Output:
Output:
 Note:
Note: A Butterworth filter of order 1 has no ringing artifact. Generally ringing is imperceptible in filters of order 2. But it can become a significant factor in filters of a higher order. For a specific cut-off frequency, ringing increases with an increase in the filter order.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...