Linear Regression Using Tensorflow
Last Updated :
03 Apr, 2023
We will briefly summarize Linear Regression before implementing it using TensorFlow. Since we will not get into the details of either Linear Regression or Tensorflow, please read the following articles for more details:
Brief Summary of Linear Regression
Linear Regression is a very common statistical method that allows us to learn a function or relationship from a given set of continuous data. For example, we are given some data points of x and corresponding y and we need to learn the relationship between them which is called a hypothesis.
In the case of Linear regression, the hypothesis is a straight line, i.e, 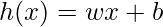 Where w is a vector called Weights and b is a scalar called Bias. The Weights and Bias are called the parameters of the model.
Where w is a vector called Weights and b is a scalar called Bias. The Weights and Bias are called the parameters of the model.
All we need to do is estimate the value of w and b from the given set of data such that the resultant hypothesis produces the least cost J which is defined by the following cost function 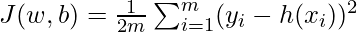 where m is the number of data points in the given dataset. This cost function is also called Mean Squared Error.
where m is the number of data points in the given dataset. This cost function is also called Mean Squared Error.
For finding the optimized value of the parameters for which J is minimum, we will be using a commonly used optimizer algorithm called Gradient Descent. Following is the pseudo-code for Gradient Descent:
Repeat until Convergence { w = w – α * δJ/δw b = b – α * δJ/δb}where α is a hyperparameter called the Learning Rate.
Linear regression is a widely used statistical method for modeling the relationship between a dependent variable and one or more independent variables. TensorFlow is a popular open-source software library for data processing, machine learning, and deep learning applications. Here are some advantages and disadvantages of using Tensorflow for linear regression:
Advantages:
Scalability: Tensorflow is designed to handle large datasets and can easily scale up to handle more data and more complex models.
Flexibility: Tensorflow provides a flexible API that allows users to customize their models and optimize their algorithms.
Performance: Tensorflow can run on multiple GPUs and CPUs, which can significantly speed up the training process and improve performance.
Integration: Tensorflow can be integrated with other open-source libraries like Numpy, Pandas, and Matplotlib, which makes it easier to preprocess and visualize data.
Disadvantages:
Complexity: Tensorflow has a steep learning curve and requires a good understanding of machine learning and deep learning concepts.
Computational resources: Running Tensorflow on large datasets requires high computational resources, which can be expensive.
Debugging: Debugging errors in Tensorflow can be challenging, especially when working with complex models.
Overkill for simple models: Tensorflow can be overkill for simple linear regression models and may not be necessary for smaller datasets.
Overall, using Tensorflow for linear regression has many advantages, but it also has some disadvantages. When deciding whether to use Tensorflow or not, it is essential to consider the complexity of the model, the size of the dataset, and the available computational resources.
Tensorflow
Tensorflow is an open-source computation library made by Google. It is a popular choice for creating applications that require high-end numerical computations and/or need to utilize Graphics Processing Units for computation purposes. These are the main reasons due to which Tensorflow is one of the most popular choices for Machine Learning applications, especially Deep Learning. It also has APIs like Estimator which provide a high level of abstraction while building Machine Learning Applications. In this article, we will not be using any high-level APIs, rather we will be building the Linear Regression model using low-level Tensorflow in the Lazy Execution Mode during which Tensorflow creates a Directed Acyclic Graph or DAG which keeps track of all the computations, and then executes all the computations done inside a Tensorflow Session.
Implementation
We will start by importing the necessary libraries. We will use Numpy along with Tensorflow for computations and Matplotlib for plotting.
Python3
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
|
In order to make the random numbers predictable, we will define fixed seeds for both Numpy and Tensorflow.
Now, let us generate some random data for training the Linear Regression Model.
Python3
x = np.linspace(0, 50, 50)
y = np.linspace(0, 50, 50)
x += np.random.uniform(-4, 4, 50)
y += np.random.uniform(-4, 4, 50)
n = len(x)
|
Let us visualize the training data.
Python3
plt.scatter(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title("Training Data")
plt.show()
|
Output:
Now we will start creating our model by defining the placeholders X and Y, so that we can feed our training examples X and Y into the optimizer during the training process.
Python3
X = tf.placeholder("float")
Y = tf.placeholder("float")
|
Now we will declare two trainable Tensorflow Variables for the Weights and Bias and initializing them randomly using np.random.randn().
Python3
W = tf.Variable(np.random.randn(), name = "W")
b = tf.Variable(np.random.randn(), name = "b")
|
Now we will define the hyperparameters of the model, the Learning Rate and the number of Epochs.
Python3
learning_rate = 0.01
training_epochs = 1000
|
Now, we will be building the Hypothesis, the Cost Function, and the Optimizer. We won’t be implementing the Gradient Descent Optimizer manually since it is built inside Tensorflow. After that, we will be initializing the Variables.
Python3
y_pred = tf.add(tf.multiply(X, W), b)
cost = tf.reduce_sum(tf.pow(y_pred-Y, 2)) / (2 * n)
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)
init = tf.global_variables_initializer()
|
Now we will begin the training process inside a Tensorflow Session.
Python3
with tf.Session() as sess:
sess.run(init)
for epoch in range(training_epochs):
for (_x, _y) in zip(x, y):
sess.run(optimizer, feed_dict = {X : _x, Y : _y})
if (epoch + 1) % 50 == 0:
c = sess.run(cost, feed_dict = {X : x, Y : y})
print("Epoch", (epoch + 1), ": cost =", c, "W =", sess.run(W), "b =", sess.run(b))
training_cost = sess.run(cost, feed_dict ={X: x, Y: y})
weight = sess.run(W)
bias = sess.run(b)
|
Output:
Now let us look at the result.
Python3
predictions = weight * x + bias
print("Training cost =", training_cost, "Weight =", weight, "bias =", bias, '\n')
|
Output:
Note that in this case both the Weight and bias are scalars. This is because, we have considered only one dependent variable in our training data. If we have m dependent variables in our training dataset, the Weight will be an m-dimensional vector while bias will be a scalar.
Finally, we will plot our result.
Python3
plt.plot(x, y, 'ro', label ='Original data')
plt.plot(x, predictions, label ='Fitted line')
plt.title('Linear Regression Result')
plt.legend()
plt.show()
|
Output:
Share your thoughts in the comments
Please Login to comment...