Law of Sine and Cosine
Last Updated :
14 Feb, 2024
Law of Sine and Cosine are the basic laws or rules used in trigonometry that are used to give the relation between sides and angles of the triangle. In this article, we will learn about the Law of Sine (Sine Rule), Sine Rule Formula, Law of Cosine (Cosine Rule), Cosine Rule Formula, and others in detail.
What is Law of Sine?
Law of Sine Formula or Sine rule is the ratio of sides and angles of a given triangle. The law of sines formula is generally used to evaluate the unknown sides or angles of a triangle. The sine rule or law of sine is the fundamental rule of trigonometry, that is used to form trigonometric problems.
Law of Sine Formula
Law of the Sine Formula in trigonometry is given by :
a / sin A = b / sin B = c / sin C
where,
- a, b, and c are Sides of Triangle
- A, B, and C are Angles of Triangle
Law of Sine Proof
Let’s take a right-angled triangle ABC with its sides,
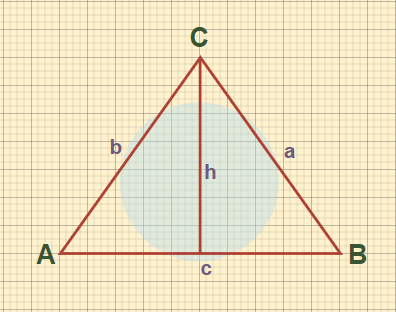
Law of Sine Proof
Draw a perpendicular CD from the base of the triangle i.e. AB. Hence, the height of the triangle is CD = h
To evaluate, a/b = sin A/Sin B
In triangle CDA,
sinA = h/b
In triangle CDB
sinB = h/a
Now,
sin A/sin B = (h/b)/(h/a)
Thus,
Sin A/Sin B = a/b
Similarly,
a/b = sinA/sinB
b/c = sinB/sinC
Thus,
a : b : c = sin A : sin B : sin C
a / sin A = b / sin B = c / sin C
What is Law of Cosine?
Law of cosine or Cosine Rule relates the lengths of sides and Cosines of Angles of the given triangle. The Law of Cosine states that “Square of any one side of a triangle is equal to the difference between the sum of squares of other sides and double the product of other sides and cosine angle included between them.”
Law of Cosine Formula
Law of Cosines formula is the formula that gives the relation between all three sides and the angle of the triangle. The law of cosines formula is,
- a2 = b2+ c2 – 2bc. cosA
- b2 = c2 + a2 – 2ca. cosB
- c2 = a2 + b2 – 2ab. cosC
where,
- a, b, and c are Lengths of sides of triangle
- A, B, and C are angles of triangle
Learn More :
Law of Cosine Proof
Let us suppose a triangle ABC with sides
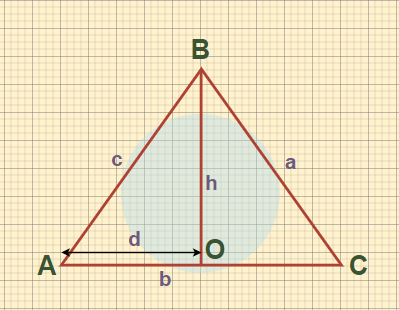
Law of Cosine Proof
Draw a perpendicular OB from the base of the triangle i.e. AC. Hence, the height of the given triangle is OB = h
Now, In ΔABO
sin A = BO/AB = h/c…(i)
cos A = AO/AB = d/c…(ii)
From equations (i) and (ii)
h = c(sinA)
d = c(cosA)
By using Pythagoras theorem in BOC
a2 = h2+ (b-d)2
Substituting values of h and d,
a2 = c2sin2A + b2 + c2cos2A – 2bc. cosA
a2 = c2(sin2A + cos2A) + b2 – 2bc.cosA
a2 = c2 + b2 – 2bc.cosA
Similarly we can prove,
- b2 = c2 + a2 – 2ca.cosB
- c2 = a2 + b2 – 2ab.cosC
The formula of Law of sine and cosine is tabulated below:
|
Table of Law of Sine and Cosine Formula
|
|
Law of Sine and Cosine
|
Formula
|
|
Law of Sine
|
a : b : c = sin A : sin B : sin C
|
|
a / sin A = b / sin B = c / sin C
|
|
Law of Cosine
|
a2 = b2+ c2 – 2bc. cosA
|
|
b2 = c2 + a2 – 2ca. cosB
|
|
c2 = a2 + b2 – 2ab. cosC
|
Related :
Examples on Law of Sine and Cosine
Example 1: Find the missing side of a triangle having its two sides 12 cm and 8 cm with the angle between them measuring 60°.
Solution:
Given,
- b = 12 cm
- c = 8 cm
- Angle between b and c (A) = 60°
Using Law of Cosine Formula
a2 = b2 + c2 – 2bc. cosA
=>a2 = (12)2 + (8)2 – 2(12)(8)cos60°
=>a2 = 144 + 64 – 192×0.5
=>a2 = 208-96
=>a2 = 112
=>a = 10.58cm
Thus, remaining side of the triangle is 10.58 cm
Example 2: Find the missing side of a triangle having its two sides 25 cm and 10 cm with the angle between them measuring 30°.
Solution:
Given,
- b = 25 cm
- c = 10 cm
- Angle between b and c (A) = 30°
Using Law of Cosine Formula
a2 = b2 + c2 – 2bc. cosA
=>a2 = (25)2 + (10)2 – 2(25)(10)cos30°
=>a2 = 625 + 100 – 500 × 0.86
=>a2 = 725 – 430
=>a2 = 295
=>a = 17.17 cm
Thus, remaining side of the triangle is 17.17 cm
Example 3: Find the missing side of a triangle having other two sides 21 cm and 14 cm with the angle between them equal to 45°.
Solution:
Given
- b = 21 cm
- c = 14 cm
- Angle between b and c (A) = 45°
Using Law of Cosine Formula
a2 = b2 + c2 – 2bc. cosA
=>a2 = (21)2 + (14)2 – 2(21)(14)cos45°
=>a2=441 + 196 – 588 × .707
=>a2 = 637 – 415.7
=>a2 = 221.3
=>a = 14.87 cm
Thus, remaining side of the triangle is 14.87 cm
Practice Questions on Law of Sin and Cos
Q1. Find the value of side a, if the two angles of a triangle are ∠A = 45° and ∠B = 30° and the side between them is b = 6 cm.
Q2. Find the missing side of a triangle having other two sides 12 cm and 9 cm with the angle between them equal to 60°.
Q3. Find the missing side of a triangle having other two sides 11 cm and 5 cm with the angle between them equal to 45°.
Q4. Find the value of side a, if the two angles of a triangle are ∠A = 30° and ∠B = 90° and the side between them is b = 20 cm.
FAQs on Law of Sine and Cosine
What is Law of Sine?
Law of sine is the fundamental law of mathematics that gives the relation between sides and the angles of the triangle.
What is Law of Sine Formula?
Law of sine formula is added below,
a/sinA = b/sinB = c/sinC
What is Law of Cosine?
Law of Cosine in mathematics is the fundamental law in trigonometry that is used to give the relation between the three sides of a triangle and any one angle of the triangle.
What is Law of Cosine Formula?
Law of cosines formulas are added below,
- a2 = b2+ c2 – 2bc. cosA
- b2 = c2 + a2 – 2ca. cosB
- c2 = a2 + b2 – 2ab. cosC
Share your thoughts in the comments
Please Login to comment...