Largest sphere that can be inscribed inside a cube
Last Updated :
11 Jul, 2022
Given here is a cube of side length a, the task is to find the biggest sphere that can be inscribed within it.
Examples:
Input: a = 4
Output: 2
Input: a = 5
Output: 2.5
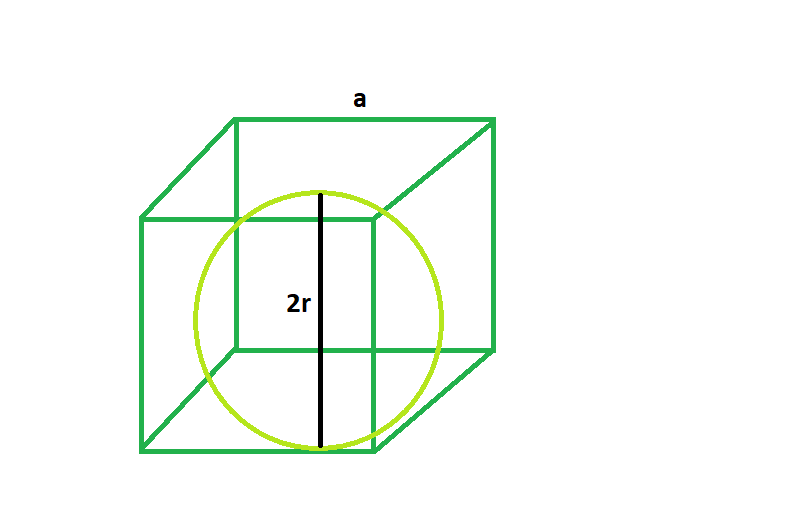
Approach:
From the 2d diagram it is clear that, 2r = a,
where, a = side of the cube
r = radius of the sphere
so r = a/2.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float sphere(float a)
{
if (a < 0)
return -1;
float r = a / 2;
return r;
}
int main()
{
float a = 5;
cout << sphere(a) << endl;
return 0;
}
|
Java
class GFG{
static float sphere(float a)
{
if (a < 0)
return -1;
float r = a / 2;
return r;
}
public static void main(String[] args)
{
float a = 5;
System.out.println(sphere(a));
}
}
|
Python3
def sphere(a):
if (a < 0):
return -1
r = a / 2
return r
if __name__ == '__main__':
a = 5
print(sphere(a))
|
C#
using System;
class GFG
{
static float sphere(float a)
{
if (a < 0)
return -1;
float r = a / 2;
return r;
}
static public void Main ()
{
float a = 5;
Console.WriteLine(sphere(a));
}
}
|
PHP
<?php
function sphere($a)
{
if ($a < 0)
return -1;
$r = ($a / 2);
return $r;
}
$a = 5;
echo sphere($a);
?>
|
Javascript
<script>
function sphere(a)
{
if (a < 0)
return -1;
var r = a / 2;
return r;
}
var a = 5;
document.write(sphere(a));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...