Largest right circular cone that can be inscribed within a sphere

Given sphere of radius 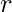. The task is to find the radius of base and height of the largest right circular cone that can be inscribed within it.
Examples: 

Input : R = 10
Output : r = 9.42809, h = 13.3333

Input : R = 25
Output : r = 23.5702, h = 33.3333

Approach:
Let the radius of the cone = r
height of the cone = h
From the diagram it is clear that: 
x = ?(R^2 – r^2) and h=x+R
Now using these values we get, 

To maximize the volume of the cone(V): 
V = (?r²h)/3
From the diagram, 
V = (?r²R)/3 + ?r²?(R² – r²)/3
Taking first derivative of V with respect to r we get, 

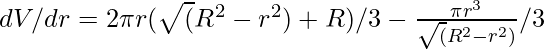
Now, setting dV/dr = 0 we get, 



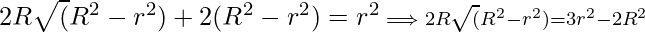
Squaring both sides and solving we get, 


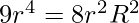
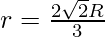
since, h = R + ?(R² – r²)
Now calculating the second derivative we get 

Thus r=(2R?2)/3 is point of maxima 
So, h = 4R/3

Below is the implementation of the above approach: 

C++

// C++ Program to find the biggest cone
// that can be inscribed within a sphere
#include <bits/stdc++.h>
using namespace std;

// Function to find the radius of the cone
float coner(float R)
{

    // radius cannot be negative
    if (R < 0)
        return -1;

    // radius of the cone
    float r = (2 * sqrt(2) * R) / 3;
    return r;
}

// Function to find the height of the cone
float coneh(float R)
{

    // side cannot be negative
    if (R < 0)
        return -1;

    // height of the cone
    float h = (4 * R) / 3;
    return h;
}

// Driver code
int main()
{
    float R = 10;

    cout << "r = " << coner(R) << ", "
         << "h = " << coneh(R) << endl;

    return 0;
}

Java

// Java Program to find the biggest cone
// that can be inscribed within a sphere
import java.util.*;
import java.lang.*;

class GFG
{
// Function to find the radius
// of the cone
static float coner(float R)
{
    // radius cannot be negative
    if (R < 0)
        return -1;

    // radius of the cone
    float r = (float)(2 *
            Math.sqrt(2) * R) / 3;
    return r;
}

// Function to find the
// height of the cone
static float coneh(float R)
{

    // side cannot be negative
    if (R < 0)
        return -1;

    // height of the cone
    float h = (4 * R) / 3;
    return h;
}

// Driver code
public static void main(String args[])
{
    float R = 10;

    System.out.println("r = " + coner(R) +
                       ", " + "h = " + coneh(R));
}
}

// This code is contributed
// by Akanksha Rai

Python3

# Python 3 Program to find the biggest cone
# that can be inscribed within a sphere
import math

# Function to find the radius
# of the cone
def coner(R):

    # radius cannot be negative
    if (R < 0):
        return -1;

    # radius of the cone
    r = (2 * math.sqrt(2) * R) / 3
    return float(r)

# Function to find the height
# of the cone
def coneh(R):

    # side cannot be negative
    if (R < 0):
        return -1;

    # height of the cone
    h = (4 * R) / 3
    return float(h)

# Driver code
R = 10
print("r = " , coner(R) ,
      ", ", "h = " , coneh(R))

# This code is contributed
# by 29AjayKumar

C#

// C# Program to find the biggest cone
// that can be inscribed within a sphere
using System;

class GFG
{
// Function to find the radius
// of the cone
static float coner(float R)
{
    // radius cannot be negative
    if (R < 0)
        return -1;

    // radius of the cone
    float r = (float)(2 *
               Math.Sqrt(2) * R) / 3;
    return r;
}

// Function to find the
// height of the cone
static float coneh(float R)
{

    // side cannot be negative
    if (R < 0)
        return -1;

    // height of the cone
    float h = (4 * R) / 3;
    return h;
}

// Driver code
public static void Main()
{
    float R = 10;

    Console.WriteLine("r = " + coner(R) +
                      ", " + "h = " + coneh(R));
}
}

// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP Program to find the biggest
// cone that can be inscribed
// within a sphere

// Function to find the radius
// of the cone
function coner($R)
{

    // radius cannot be negative
    if ($R < 0)
        return -1;

    // radius of the cone
    $r = (2 * sqrt(2) * $R) / 3;
    return $r;
}

// Function to find the height
// of the cone
function coneh($R)
{

    // side cannot be negative
    if ($R < 0)
        return -1;

    // height of the cone
    $h = (4 * $R) / 3;
    return $h;
}

// Driver code
$R = 10;

echo ("r = ");
echo coner($R);
echo (", ");
echo ("h = ");
echo (coneh($R));

// This code is contributed
// by Shivi_Aggarwal
?>

Javascript

<script>
// javascript Program to find the biggest cone
// that can be inscribed within a sphere

// Function to find the radius
// of the cone
function coner(R)
{

    // radius cannot be negative
    if (R < 0)
        return -1;

    // radius of the cone
    var r = (2 *
            Math.sqrt(2) * R) / 3;
    return r;
}

// Function to find the
// height of the cone
function coneh(R)
{

    // side cannot be negative
    if (R < 0)
        return -1;

    // height of the cone
    var h = (4 * R) / 3;
    return h;
}

// Driver code
var R = 10;
document.write("r = " + coner(R).toFixed(5) +
                   ", " + "h = " + coneh(R).toFixed(5));

// This code is contributed by 29AjayKumar
</script>

Output:

r = 9.42809, h = 13.3333

Time Complexity: O(1)

Auxiliary Space: O(1), since no extra space has been taken.