Largest right circular cone that can be inscribed within a sphere

Last Updated : 17 Mar, 2021

Given sphere of radius 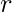$r$ . The task is to find the radius of base and height of the largest right circular cone that can be inscribed within it.
Examples:

Input : R = 10
Output : r = 9.42809, h = 13.3333

Input : R = 25
Output : r = 23.5702, h = 33.3333

Approach:
Let the radius of the cone = r
height of the cone = h
From the diagram it is clear that:
x = √(R^2 – r^2) and h=x+R
Now using these values we get,

To maximize the volume of the cone(V):
V = (πr²h)/3
From the diagram,
V = (πr²R)/3 + πr²√(R² – r²)/3
Taking first derivative of V with respect to r we get,
$dV/dr = 2\pi r(\sqrt(R^2 - r^2) + R)/3 - \frac{\pi r^3}{\sqrt(R^2 - r^2)}/3$
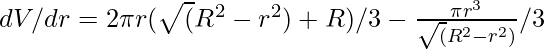
Now, setting dV/dr = 0 we get,
$\frac{2\pi r}{3}[R+\sqrt(R^2-r^2)] =\frac{ \pi r^3}{3\sqrt(R^2 - r^2}$
$2[R+\sqrt(R^2-r^2)] =\frac{r^2}{\sqrt(R^2 - r^2)}$
$2R\sqrt(R^2 - r^2)}+2(R^2 - r^2)=r^2\scriptstyle\implies 2R\sqrt(R^2 - r^2)}=3r^2 - 2R^2$
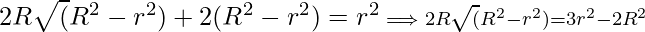
Squaring both sides and solving we get,
$9r^4=8r^2 R^2$
$r=\frac{2\sqrt{2}R}{3}$
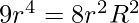
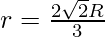
since, h = R + √(R² – r²)
Now calculating the second derivative we get
*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty
Thus r=(2R√2)/3 is point of maxima
So, h = 4R/3

Below is the implementation of the above approach:

C++

// C++ Program to find the biggest cone
// that can be inscribed within a sphere
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the radius of the cone
float coner(float R)
{
 
    // radius cannot be negative
    if (R < 0)
        return -1;
 
    // radius of the cone
    float r = (2 * sqrt(2) * R) / 3;
    return r;
}
 
// Function to find the height of the cone
float coneh(float R)
{
 
    // side cannot be negative
    if (R < 0)
        return -1;
 
    // height of the cone
    float h = (4 * R) / 3;
    return h;
}
 
// Driver code
int main()
{
    float R = 10;
 
    cout << "r = " << coner(R) << ", "
         << "h = " << coneh(R) << endl;
 
    return 0;
}

Java

// Java Program to find the biggest cone
// that can be inscribed within a sphere
import java.util.*;
import java.lang.*;
 
class GFG
{
// Function to find the radius
// of the cone
static float coner(float R)
{
    // radius cannot be negative
    if (R < 0)
        return -1;
 
    // radius of the cone
    float r = (float)(2 *
            Math.sqrt(2) * R) / 3;
    return r;
}
 
// Function to find the
// height of the cone
static float coneh(float R)
{
 
    // side cannot be negative
    if (R < 0)
        return -1;
 
    // height of the cone
    float h = (4 * R) / 3;
    return h;
}
 
// Driver code
public static void main(String args[])
{
    float R = 10;
 
    System.out.println("r = " + coner(R) +
                       ", " + "h = " + coneh(R));
}
}
 
// This code is contributed
// by Akanksha Rai

Python3

# Python 3 Program to find the biggest cone
# that can be inscribed within a sphere
import math
 
# Function to find the radius
# of the cone
def coner(R):
     
    # radius cannot be negative
    if (R < 0):
        return -1;
     
    # radius of the cone
    r = (2 * math.sqrt(2) * R) / 3
    return float(r)
 
# Function to find the height
# of the cone
def coneh(R):
     
    # side cannot be negative
    if (R < 0):
        return -1;
 
    # height of the cone
    h = (4 * R) / 3
    return float(h)
 
# Driver code
R = 10
print("r = " , coner(R) ,
      ", ", "h = " , coneh(R))
 
# This code is contributed
# by 29AjayKumar

C#

// C# Program to find the biggest cone
// that can be inscribed within a sphere
using System;
 
class GFG
{
// Function to find the radius
// of the cone
static float coner(float R)
{
    // radius cannot be negative
    if (R < 0)
        return -1;
 
    // radius of the cone
    float r = (float)(2 *
               Math.Sqrt(2) * R) / 3;
    return r;
}
 
// Function to find the
// height of the cone
static float coneh(float R)
{
 
    // side cannot be negative
    if (R < 0)
        return -1;
 
    // height of the cone
    float h = (4 * R) / 3;
    return h;
}
 
// Driver code
public static void Main()
{
    float R = 10;
 
    Console.WriteLine("r = " + coner(R) +
                      ", " + "h = " + coneh(R));
}
}
 
// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP Program to find the biggest
// cone that can be inscribed
// within a sphere
 
// Function to find the radius
// of the cone
function coner($R)
{
 
    // radius cannot be negative
    if ($R < 0)
        return -1;
 
    // radius of the cone
    $r = (2 * sqrt(2) * $R) / 3;
    return $r;
}
 
// Function to find the height
// of the cone
function coneh($R)
{
 
    // side cannot be negative
    if ($R < 0)
        return -1;
 
    // height of the cone
    $h = (4 * $R) / 3;
    return $h;
}
 
// Driver code
$R = 10;
 
echo ("r = ");
echo coner($R);
echo (", ");
echo ("h = ");
echo (coneh($R));
 
// This code is contributed
// by Shivi_Aggarwal
?>

Javascript

<script>
// javascript Program to find the biggest cone
// that can be inscribed within a sphere
 
// Function to find the radius
// of the cone
function coner(R)
{
 
    // radius cannot be negative
    if (R < 0)
        return -1;
 
    // radius of the cone
    var r = (2 *
            Math.sqrt(2) * R) / 3;
    return r;
}
 
// Function to find the
// height of the cone
function coneh(R)
{
 
    // side cannot be negative
    if (R < 0)
        return -1;
 
    // height of the cone
    var h = (4 * R) / 3;
    return h;
}
 
// Driver code
var R = 10;
document.write("r = " + coner(R).toFixed(5) +
                   ", " + "h = " + coneh(R).toFixed(5));
 
// This code is contributed by 29AjayKumar
</script>

Output:

r = 9.42809, h = 13.3333

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live

My Personal Notes

Related Articles

C++

Java

Python3

C#

PHP

Javascript