Largest right circular cylinder that can be inscribed within a cone
Last Updated :
29 Feb, 2024
Given a right circular cylinder which is inscribed in a cone of height h and base radius r. The task is to find the largest possible volume of the cylinder.
Examples:
Input: r = 4, h = 8
Output: 119.087
Input: r = 5, h = 9
Output: 209.333
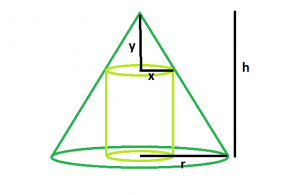
Approach: The volume of a cylinder is V = ?r^2h
In this problem, first derive an equation for volume using similar triangles in terms of the height and radius of the cone. Once we have the modified the volume equation, we’ll take the derivative of the volume and solve for the largest value.
Let x be the radius of the cylinder and y be the distance from the top of the cone to the top of the inscribed cylinder. Therefore, the height of the cylinder is h – y
The volume of the inscribed cylinder is V = ?x^2(h-y).
We use the method of similar ratios to find a relationship between the height and radius, h-y and x.
y/x = h/r
y = hx/r
Substitute the equation for y into the equation for volume, V.
V = ?x^2(h-y)
V = ?x^2(h-hx/r)
V = ?x^2h – ?x^3h/r
now, dV/dx = d(?x^2h – ?x^3h/r)/dx
and setting dV/dx = 0
we get, x = 0, 2r/3
So, x = 2r/3
and, y = 2h/3
So, V = ?8r^2h/27
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float cyl(float r, float h)
{
if (r < 0 && h < 0)
return -1;
float R = (2 * r) / 3;
float H = (2 * h) / 3;
float V = 3.14 * pow(R, 2) * H;
return V;
}
int main()
{
float r = 4, h = 8;
cout << cyl(r, h) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static double cyl(double r, double h)
{
if (r < 0 && h < 0)
return -1;
double R = (2 * r) / 3;
double H = (2 * h) / 3;
double V = 3.14 * Math.pow(R, 2) * H;
return V;
}
public static void main (String[] args) {
double r = 4, h = 8;
System.out.println (cyl(r, h));
}
}
|
Python 3
import math
def cyl(r, h):
if (r < 0 and h < 0):
return -1
R = (2 * r) / 3
H = (2 * h) / 3
V = 3.14 * math.pow(R, 2) * H
return V
r = 4; h = 8;
print(cyl(r, h), "\n")
|
C#
using System;
class GFG
{
static double cyl(double r, double h)
{
if (r < 0 && h < 0)
return -1;
double R = (2 * r) / 3;
double H = (2 * h) / 3;
double V = 3.14 * Math.Pow(R, 2) * H;
return V;
}
static public void Main ()
{
double r = 4, h = 8;
Console.WriteLine(cyl(r, h));
}
}
|
Javascript
<script>
function cyl(r , h)
{
if (r < 0 && h < 0)
return -1;
var R = (2 * r) / 3;
var H = (2 * h) / 3;
var V = 3.14 * Math.pow(R, 2) * H;
return V;
}
var r = 4, h = 8;
document.write(cyl(r, h).toFixed(5));
</script>
|
PHP
<?php
function cyl($r, $h)
{
if ($r < 0 && $h < 0)
return -1;
$R = (int)(2 * $r) / 3;
$H = (int)(2 * $h) / 3;
$V = 3.14 * pow($R, 2) * $H;
return $V;
}
$r = 4;
$h = 8;
echo cyl($r, $h);
?>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...