K’th Smallest/Largest Element in Unsorted Array | Worst case Linear Time
Last Updated :
18 Sep, 2023
We recommend reading the following posts as a prerequisite for this post.
K’th Smallest/Largest Element in Unsorted Array
K’th Smallest/Largest Element in Unsorted Array | Expected Linear Time
Given an array and a number k where k is smaller than the size of the array, we need to find the k’th smallest element in the given array. It is given that all array elements are distinct.
Examples:
Input: arr[] = {7, 10, 4, 3, 20, 15}
k = 3
Output: 7
Input: arr[] = {7, 10, 4, 3, 20, 15}
k = 4
Output: 10
In the previous post, we discussed an expected linear time algorithm. In this post, a worst-case linear time method is discussed. The idea in this new method is similar to quickSelect(). We get worst-case linear time by selecting a pivot that divides the array in a balanced way (there are not very few elements on one side and many on another side). After the array is divided in a balanced way, we apply the same steps as used in quickSelect() to decide whether to go left or right of the pivot.
Following is the complete algorithm.
kthSmallest(arr[0..n-1], k)
1) Divide arr[] into ?n/5? groups where size of each group is 5 except possibly the last group which may have less than 5 elements.
2) Sort the above created ?n/5? groups and find median of all groups. Create an auxiliary array ‘median[]’ and store medians of all ?n/5? groups in this median array.
// Recursively call this method to find median of median[0..?n/5?-1]
3) medOfMed = kthSmallest(median[0..?n/5?-1], ?n/10?)
4) Partition arr[] around medOfMed and obtain its position.
pos = partition(arr, n, medOfMed)
5) If pos == k return medOfMed
6) If pos > k return kthSmallest(arr[l..pos-1], k)
7) If pos < k return kthSmallest(arr[pos+1..r], k-pos+l-1)
In the above algorithm, the last 3 steps are the same as the algorithm in the previous post. The first four steps are used to obtain a good point for partitioning the array (to ensure there are not too many elements on either side of the pivot).
Following is the implementation of the above algorithm.
C++
#include<bits/stdc++.h>
using namespace std;
int partition(int arr[], int l, int r, int k);
int findMedian(int arr[], int n)
{
sort(arr, arr+n);
return arr[n/2];
}
int kthSmallest(int arr[], int l, int r, int k)
{
if (k > 0 && k <= r - l + 1)
{
int n = r-l+1;
int i, median[(n+4)/5];
for (i=0; i<n/5; i++)
median[i] = findMedian(arr+l+i*5, 5);
if (i*5 < n)
{
median[i] = findMedian(arr+l+i*5, n%5);
i++;
}
int medOfMed = (i == 1)? median[i-1]:
kthSmallest(median, 0, i-1, i/2);
int pos = partition(arr, l, r, medOfMed);
if (pos-l == k-1)
return arr[pos];
if (pos-l > k-1)
return kthSmallest(arr, l, pos-1, k);
return kthSmallest(arr, pos+1, r, k-pos+l-1);
}
return INT_MAX;
}
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
int partition(int arr[], int l, int r, int x)
{
int i;
for (i=l; i<r; i++)
if (arr[i] == x)
break;
swap(&arr[i], &arr[r]);
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(&arr[i], &arr[j]);
i++;
}
}
swap(&arr[i], &arr[r]);
return i;
}
int main()
{
int arr[] = {12, 3, 5, 7, 4, 19, 26};
int n = sizeof(arr)/sizeof(arr[0]), k = 3;
cout << "K'th smallest element is "
<< kthSmallest(arr, 0, n-1, k);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int findMedian(int arr[], int i,int n)
{
Arrays.sort(arr, i, n);
return arr[i+(n-i)/2];
}
static int kthSmallest(int arr[], int l, int r, int k)
{
if (k > 0 && k <= r - l + 1)
{
int n = r - l + 1 ;
int i;
int []median = new int[(n + 4) / 5];
for (i = 0; i < n/5; i++)
median[i] = findMedian(arr, l+i*5, l+i*5+5);
if (i*5 < n)
{
median[i] = findMedian(arr, l+i*5, l+i*5+n%5);
i++;
}
int medOfMed = (i == 1)? median[i - 1]:
kthSmallest(median, 0, i - 1, i / 2);
int pos = partition(arr, l, r, medOfMed);
if (pos-l == k - 1)
return arr[pos];
if (pos-l > k - 1)
return kthSmallest(arr, l, pos - 1, k);
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
return Integer.MAX_VALUE;
}
static int[] swap(int []arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
static int partition(int arr[], int l,
int r, int x)
{
int i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
public static void main(String[] args)
{
int arr[] = {12, 3, 5, 7, 4, 19, 26};
int n = arr.length, k = 3;
System.out.println("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
}
}
|
Python3
def kthSmallest(arr, l, r, k):
if (k > 0 and k <= r - l + 1):
n = r - l + 1
median = []
i = 0
while (i < n // 5):
median.append(findMedian(arr, l + i * 5, 5))
i += 1
if (i * 5 < n):
median.append(findMedian(arr, l + i * 5,
n % 5))
i += 1
if i == 1:
medOfMed = median[i - 1]
else:
medOfMed = kthSmallest(median, 0,
i - 1, i // 2)
pos = partition(arr, l, r, medOfMed)
if (pos - l == k - 1):
return arr[pos]
if (pos - l > k - 1):
return kthSmallest(arr, l, pos - 1, k)
return kthSmallest(arr, pos + 1, r,
k - pos + l - 1)
return 999999999999
def swap(arr, a, b):
temp = arr[a]
arr[a] = arr[b]
arr[b] = temp
def partition(arr, l, r, x):
for i in range(l, r):
if arr[i] == x:
swap(arr, r, i)
break
x = arr[r]
i = l
for j in range(l, r):
if (arr[j] <= x):
swap(arr, i, j)
i += 1
swap(arr, i, r)
return i
def findMedian(arr, l, n):
lis = []
for i in range(l, l + n):
lis.append(arr[i])
lis.sort()
return lis[n // 2]
if __name__ == '__main__':
arr = [12, 3, 5, 7, 4, 19, 26]
n = len(arr)
k = 3
print("K'th smallest element is",
kthSmallest(arr, 0, n - 1, k))
|
C#
using System;
class GFG
{
static int findMedian(int []arr, int i, int n)
{
if(i <= n)
Array.Sort(arr, i, n);
else
Array.Sort(arr, n, i);
return arr[n/2];
}
static int kthSmallest(int []arr, int l,
int r, int k)
{
if (k > 0 && k <= r - l + 1)
{
int n = r - l + 1 ;
int i;
int []median = new int[(n + 4) / 5];
for (i = 0; i < n/5; i++)
median[i] = findMedian(arr, l + i * 5, 5);
if (i*5 < n)
{
median[i] = findMedian(arr,l + i * 5, n % 5);
i++;
}
int medOfMed = (i == 1)? median[i - 1]:
kthSmallest(median, 0, i - 1, i / 2);
int pos = partition(arr, l, r, medOfMed);
if (pos-l == k - 1)
return arr[pos];
if (pos-l > k - 1)
return kthSmallest(arr, l, pos - 1, k);
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
return int.MaxValue;
}
static int[] swap(int []arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
static int partition(int []arr, int l,
int r, int x)
{
int i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
i = l;
for (int j = l; j <= r - 1; j++)
{
if (arr[j] <= x)
{
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
public static void Main(String[] args)
{
int []arr = {12, 3, 5, 7, 4, 19, 26};
int n = arr.Length, k = 3;
Console.WriteLine("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
}
}
|
Javascript
<script>
function findMedian(arr, i, n) {
if (i <= n)
arr.sort((a, b) => a - b);
else
arr.sort((a, b) => a - b);
let flr = Math.floor(n / 2);
return arr[flr];
}
function kthSmallest(arr, l, r, k)
{
if (k > 0 && k <= r - l + 1)
{
let n = r - l + 1;
let i;
let median = new Array(Math.floor((n + 4) / 5));
for (i = 0; i < n / 5; i++)
median[i] = findMedian(arr, l + i * 5, 5);
if (i * 5 < n)
{
median[i] = findMedian(arr, l + i * 5, n % 5);
i++;
}
let medOfMed = (i == 1) ? median[i - 1] :
kthSmallest(median, 0, i - 1, Math.floor(i / 2));
let pos = partition(arr, l, r, medOfMed);
if (pos - l == k - 1)
return arr[pos];
if (pos - l > k - 1)
return kthSmallest(arr, l, pos - 1, k);
return kthSmallest(arr, pos + 1, r, k - pos + l - 1);
}
return Integer.MAX_VALUE;
}
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
function partition(arr, l, r, x) {
let i;
for (i = l; i < r; i++)
if (arr[i] == x)
break;
swap(arr, i, r);
i = l;
for (let j = l; j <= r - 1; j++) {
if (arr[j] <= x) {
swap(arr, i, j);
i++;
}
}
swap(arr, i, r);
return i;
}
let arr = [12, 3, 5, 7, 4, 19, 26];
let n = arr.length, k = 3;
document.write("K'th smallest element is "
+ kthSmallest(arr, 0, n - 1, k));
</script>
|
OutputK'th smallest element is 5
The code implements the “Worst-case linear time algorithm to find the k-th smallest element” using the Decrease and Conquer strategy. The steps of the algorithm are as follows:
If the value of k is greater than the number of elements in the array or k is less than 1, return INT_MAX (which is a constant representing the maximum value of an integer in C++).
Divide the array into groups of five elements each (except possibly the last group, which may have less than five elements). Sort each group and find its median. Store all the medians in an array called ‘median’.
Find the median of the ‘median’ array by recursively calling the kthSmallest() function. If the ‘median’ array has only one element, then it is the median of all medians.
Partition the original array around the median of medians and find the position ‘pos’ of the pivot element in the sorted array.
If pos-l is equal to k-1 (i.e., the pivot element is the k-th smallest element), return the pivot element.
If pos-l is greater than k-1, then recursively call the kthSmallest() function on the left sub-array (i.e., arr[l…pos-1]).
If pos-l is less than k-1, then recursively call the kthSmallest() function on the right sub-array (i.e., arr[pos+1…r]) with updated k value (k-(pos-l+1)).
Time Complexity:
The worst-case time complexity of the above algorithm is O(n). Let us analyze all steps.
Steps (1) and (2) take O(n) time as finding median of an array of size 5 takes O(1) time and there are n/5 arrays of size 5.
Step (3) takes T(n/5) time. Step (4) is a standard partition and takes O(n) time.
The interesting steps are 6) and 7). At most, one of them is executed. These are recursive steps. What is the worst-case size of these recursive calls? The answer is the maximum number of elements greater than medOfMed (obtained in step 3) or the maximum number of elements smaller than medOfMed.
How many elements are greater than medOfMed and how many are smaller?
At least half of the medians found in step 2 are greater than or equal to medOfMed. Thus, at least half of the n/5 groups contribute 3 elements that are greater than medOfMed, except for the one group that has fewer than 5 elements. Therefore, the number of elements greater than medOfMed is at least.
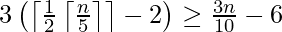
Similarly, the number of elements which are less than medOfMed is at least 3n/10 – 6. In the worst case, the function recurs for at most n – (3n/10 – 6) which is 7n/10 + 6 elements.
Note that 7n/10 + 6 < 20 and that any input of 80 or fewer elements requires O(1) time. We can therefore obtain the recurrence
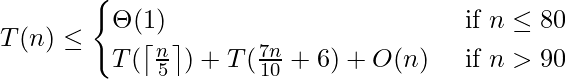
We show that the running time is linear by substitution. Assume that T(n) cn for some constant c and all n > 80. Substituting this inductive hypothesis into the right-hand side of the recurrence yields
T(n) <= cn/5 + c(7n/10 + 6) + O(n)
<= cn/5 + c + 7cn/10 + 6c + O(n)
<= 9cn/10 + 7c + O(n)
<= cn,
since we can pick c large enough so that c(n/10 – 7) is larger than the function described by the O(n) term for all n > 80. The worst-case running time of is therefore linear
Note that the above algorithm is linear in the worst case, but the constants are very high for this algorithm. Therefore, this algorithm doesn’t work well in practical situations; randomized quickSelect works much better and is preferred.
Share your thoughts in the comments
Please Login to comment...