Linear Search Algorithm – Data Structure and Algorithms Tutorials
Last Updated :
03 May, 2024
Linear Search is defined as a sequential search algorithm that starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set.
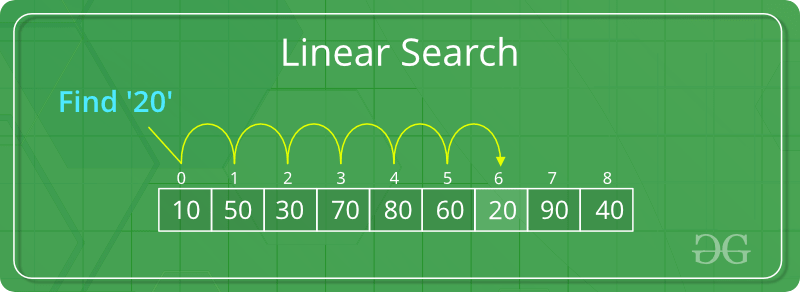
What is Linear Search?
Linear Search is a method for searching an element in a collection of elements. In Linear Search, each element of the collection is visited one by one in a sequential fashion to find the desired element. Linear Search is also known as Sequential Search.
Algorithm for Linear Search:
The algorithm for linear search can be broken down into the following steps:
- Start: Begin at the first element of the collection of elements.
- Compare: Compare the current element with the desired element.
- Found: If the current element is equal to the desired element, return true or index to the current element.
- Move: Otherwise, move to the next element in the collection.
- Repeat: Repeat steps 2-4 until we have reached the end of collection.
- Not found: If the end of the collection is reached without finding the desired element, return that the desired element is not in the array.
How Does Linear Search Algorithm Work?
In Linear Search Algorithm,
- Every element is considered as a potential match for the key and checked for the same.
- If any element is found equal to the key, the search is successful and the index of that element is returned.
- If no element is found equal to the key, the search yields “No match found”.
For example: Consider the array arr[] = {10, 50, 30, 70, 80, 20, 90, 40} and key = 30
Step 1: Start from the first element (index 0) and compare key with each element (arr[i]).
- Comparing key with first element arr[0]. SInce not equal, the iterator moves to the next element as a potential match.
![Compare key with arr[0]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161339/Linear-search-algorithm-1.webp)
Compare key with arr[0]
- Comparing key with next element arr[1]. SInce not equal, the iterator moves to the next element as a potential match.
![Compare key with arr[1]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161415/Linear-search-algorithm-2.webp)
Compare key with arr[1]
Step 2: Now when comparing arr[2] with key, the value matches. So the Linear Search Algorithm will yield a successful message and return the index of the element when key is found (here 2).
![Compare key with arr[2]](https://media.geeksforgeeks.org/wp-content/uploads/20230519161442/Linear-search-algorithm-3.webp)
Compare key with arr[2]
Implementation of Linear Search Algorithm:
In Linear Search, we iterate over all the elements of the array and check if it the current element is equal to the target element. If we find any element to be equal to the target element, then return the index of the current element. Otherwise, if no element is equal to the target element, then return -1 as the element is not found.
Below is the implementation of the linear search algorithm:
C++
// C++ code to linearly search x in arr[].
#include <bits/stdc++.h>
using namespace std;
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, N, x);
(result == -1)
? cout << "Element is not present in array"
: cout << "Element is present at index " << result;
return 0;
}
// C code to linearly search x in arr[].
#include <stdio.h>
int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
int main(void)
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int N = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, N, x);
(result == -1)
? printf("Element is not present in array")
: printf("Element is present at index %d", result);
return 0;
}
// Java code for linearly searching x in arr[].
import java.io.*;
class GFG {
public static int search(int arr[], int N, int x)
{
for (int i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
// Driver code
public static void main(String args[])
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
// Function call
int result = search(arr, arr.length, x);
if (result == -1)
System.out.print(
"Element is not present in array");
else
System.out.print("Element is present at index "
+ result);
}
}
# Python3 code to linearly search x in arr[].
def search(arr, N, x):
for i in range(0, N):
if (arr[i] == x):
return i
return -1
# Driver Code
if __name__ == "__main__":
arr = [2, 3, 4, 10, 40]
x = 10
N = len(arr)
# Function call
result = search(arr, N, x)
if(result == -1):
print("Element is not present in array")
else:
print("Element is present at index", result)
// C# code to linearly search x in arr[].
using System;
class GFG {
public static int search(int[] arr, int N, int x)
{
for (int i = 0; i < N; i++) {
if (arr[i] == x)
return i;
}
return -1;
}
// Driver's code
public static void Main()
{
int[] arr = { 2, 3, 4, 10, 40 };
int x = 10;
// Function call
int result = search(arr, arr.Length, x);
if (result == -1)
Console.WriteLine(
"Element is not present in array");
else
Console.WriteLine("Element is present at index "
+ result);
}
}
// This code is contributed by DrRoot_
// Javascript code to linearly search x in arr[].
function search(arr, n, x)
{
for (let i = 0; i < n; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length;
// Function call
let result = search(arr, n, x);
(result == -1)
? console.log("Element is not present in array")
: console.log("Element is present at index " + result);
// This code is contributed by Manoj
<?php
// PHP code for linearly search x in arr[].
function search($arr, $n, $x)
{
for($i = 0; $i < $n; $i++) {
if($arr[$i] == $x)
return $i;
}
return -1;
}
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$x = 10;
// Function call
$result = search($arr, sizeof($arr), $x);
if($result == -1)
echo "Element is not present in array";
else
echo "Element is present at index " ,
$result;
// This code is contributed
// by jit_t
?>
OutputElement is present at index 3
Time Complexity:
- Best Case: In the best case, the key might be present at the first index. So the best case complexity is O(1)
- Worst Case: In the worst case, the key might be present at the last index i.e., opposite to the end from which the search has started in the list. So the worst-case complexity is O(N) where N is the size of the list.
- Average Case: O(N)
Auxiliary Space: O(1) as except for the variable to iterate through the list, no other variable is used.
Applications of Linear Search:
- Unsorted Lists: When we have an unsorted array or list, linear search is most commonly used to find any element in the collection.
- Small Data Sets: Linear Search is preferred over binary search when we have small data sets with
- Searching Linked Lists: In linked list implementations, linear search is commonly used to find elements within the list. Each node is checked sequentially until the desired element is found.
- Simple Implementation: Linear Search is much easier to understand and implement as compared to Binary Search or Ternary Search.
Advantages of Linear Search:
- Linear search can be used irrespective of whether the array is sorted or not. It can be used on arrays of any data type.
- Does not require any additional memory.
- It is a well-suited algorithm for small datasets.
Disadvantages of Linear Search:
- Linear search has a time complexity of O(N), which in turn makes it slow for large datasets.
- Not suitable for large arrays.
When to use Linear Search?
- When we are dealing with a small dataset.
- When you are searching for a dataset stored in contiguous memory.
Frequently Asked Questions (FAQs) on Linear Search:
1. What is linear search?
Linear search, also known as sequential search, is a simple searching algorithm that traverses a list or array sequentially to find a target element. In Linear Search, we can get the
2. How does linear search work?
Linear search iterates through each element in the list or array, comparing it with the target element until a match is found or the end of the list is reached. If the end of the list is reached, then it means that the target element is not present in the array.
3. What is the time complexity of linear search?
The time complexity of linear search is O(n), where n is the number of elements in the list or array being searched. This means the time taken for searching increases linearly with the size of the input.
4. When is linear search preferred over other searching algorithms?
Linear search is preferred when the list or array is unsorted, or when the size of the input is relatively small. It’s simple to implement and doesn’t require the data to be in any specific order.
5. What are the advantages of linear search?
Linear search is easy to implement, and it works efficiently on small-sized arrays or lists. It doesn’t require any pre-processing like sorting, making it suitable for dynamic data structures.
6. What are the disadvantages of linear search?
Linear search becomes inefficient for large-sized arrays or lists, as it needs to scan through each element sequentially. It has a time complexity of O(n), which means the search time grows linearly with the size of the input.
7. How do you implement linear search in programming languages like Python, Java, or C++?
Linear search can be implemented using loops to iterate through the elements of the array or list, comparing each element with the target value until a match is found or the end of the list is reached.
8. Can linear search be applied to other data structures?
Yes, linear search can be applied not only to arrays or lists but also to other linear data structures like linked lists. The principle remains the same: iterating through each element until the target is found or the end is reached.
9. Is linear search suitable for sorted arrays or lists?
While linear search can still be used on sorted arrays or lists, it’s not the most efficient option. Binary search, for example, is more suitable for sorted data as it has a time complexity of O(log n).
10. What are some real-world applications of linear search?
Linear search can be used in scenarios such as searching for a specific value in a phone book, searching for a name in an unsorted list of contacts, or finding an item in a grocery list. It’s often used in scenarios where the data size is small or not expected to grow significantly.
Related Articles:
Share your thoughts in the comments
Please Login to comment...