Javascript Program for Kronecker Product of two matrices
Last Updated :
25 Apr, 2022
Given a 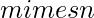 matrix A and a
matrix A and a 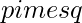 matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an
matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an 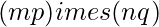 matrix.
matrix.
A tensor B = |a11B a12B|
|a21B a22B|
= |a11b11 a11b12 a12b11 a12b12|
|a11b21 a11b22 a12b21 a12b22|
|a11b31 a11b32 a12b31 a12b32|
|a21b11 a21b12 a22b11 a22b12|
|a21b21 a21b22 a22b21 a22b22|
|a21b31 a21b32 a22b31 a22b32|
Examples:
1. The matrix direct(kronecker) product of the 2×2 matrix A
and the 2×2 matrix B is given by the 4×4 matrix :
Input : A = 1 2 B = 0 5
3 4 6 7
Output : C = 0 5 0 10
6 7 12 14
0 15 0 20
18 21 24 28
2. The matrix direct(kronecker) product of the 2×3 matrix A
and the 3×2 matrix B is given by the 6×6 matrix :
Input : A = 1 2 B = 0 5 2
3 4 6 7 3
1 0
Output : C = 0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Below is the code to find the Kronecker Product of two matrices and stores it as matrix C :
Javascript
<script>
let cola = 2, rowa = 3, colb = 3, rowb = 2;
function Kroneckerproduct(A, B)
{
let C= new Array(rowa * rowb)
for(let i = 0; i < (rowa * rowb); i++)
{
C[i] = new Array(cola * colb);
for(let j = 0; j < (cola * colb); j++)
{
C[i][j] = 0;
}
}
for (let i = 0; i < rowa; i++)
{
for (let k = 0; k < rowb; k++)
{
for (let j = 0; j < cola; j++)
{
for (let l = 0; l < colb; l++)
{
C[i + l + 1][j + k + 1] = A[i][j] * B[k][l];
document.write( C[i + l + 1][j + k + 1]+" ");
}
}
document.write("</br>");
}
}
}
let A = [ [ 1, 2 ],
[ 3, 4 ],
[ 1, 0 ] ];
let B = [ [ 0, 5, 2 ],
[ 6, 7, 3 ] ];
Kroneckerproduct(A, B);
</script>
|
Output :
0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Time Complexity: O(rowa*rowb*cola*colb), as we are using nested loops.
Auxiliary Space: O((rowa + colb)*(rowb + cola)), as we are using extra space in matrix C.
Please refer complete article on Kronecker Product of two matrices for more details!
Share your thoughts in the comments
Please Login to comment...