How to Install SQLAlchemy in Python in Windows?
Last Updated :
22 Sep, 2021
SQLAlchemy is the Python SQL toolkit and Object Relational Mapper that is used as flexible database access using SQL. In this article, we will look into the process of installing SQLAlchemy on a windows machine.
Pre-requisites:
The only thing that you need for installing Numpy on Windows are:
Installing SQLAlchemy on Windows using Conda:
If you want the installation to be done through conda, open up the Anaconda Powershell Prompt and use the below command:
conda install -c anaconda sqlalchemy
Type y for yes when prompted.
You will get a similar message once the installation is complete:
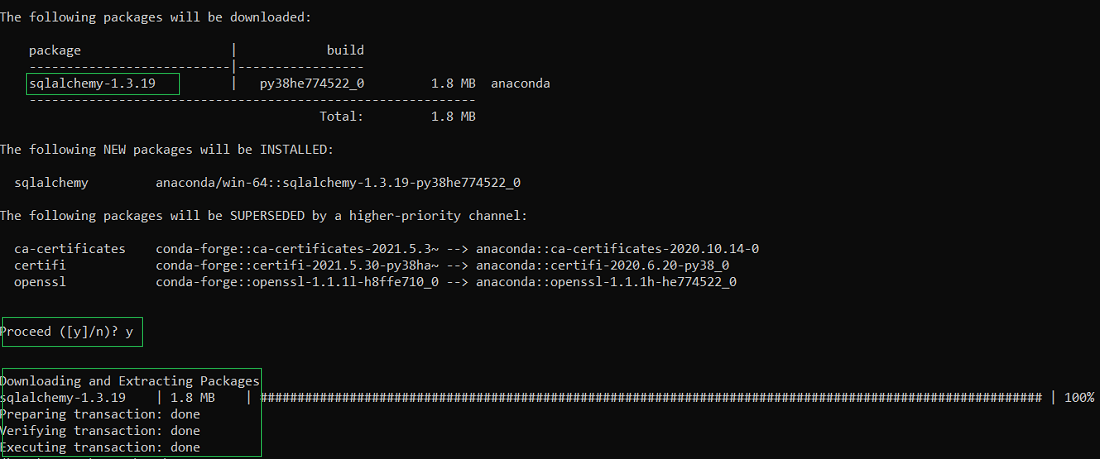
Make sure you follow the best practices for installation using conda as:
- Use an environment for installation rather than in the base environment using the below command:
conda create -n my-env
conda activate my-env
Note: If your preferred method of installation is conda-forge, use the below command:
conda config --env --add channels conda-forge
Verifying SQLAlchemy Installation on Windows using Conda:
To verify if SQLAlchemy has been successfully installed in your system run the below command in Anaconda Powershell Prompt:
conda list pyglet
You’ll get the below message if the installation is complete:

Installing SQLAlchemy on Windows using PIP:
If you want the installation to be done through PIP, open up the command Prompt and use the below command:
pip install pyglet
You will get a similar message once the installation is complete:
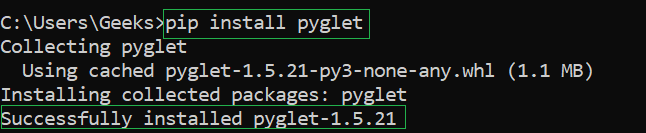
Verifying SQLAlchemy Installation on Windows using PIP:
To verify if the SQLAlchemy has been successfully installed in your system run the below command in Command Prompt:
python -m pip show sqlalchemy
You’ll get the below message if the installation is complete:
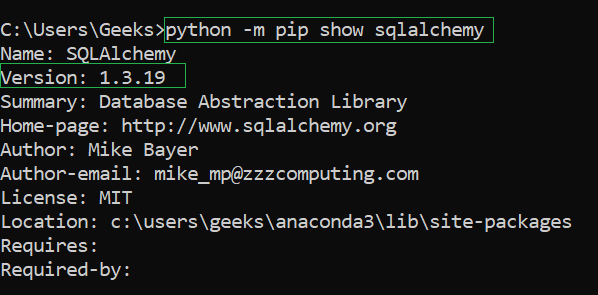
Share your thoughts in the comments
Please Login to comment...