GRE Geometry | Lines and Angles
Last Updated :
15 Feb, 2023
Lines: A Line is a one-dimensional geometrical figure having negligible breadth extending infinitely in both directions. A line may be straight or curved. A straight line has same direction throughout its whole length from point to point. A curved line changes it’s direction continuously from point to point.  Line Segment: A line segment is a part of a line having specified end points. There can be infinite number of line segments on a line. In the following diagram, AB is a denoted line segment. Two line segments having equal length are called congruent line segments.
Line Segment: A line segment is a part of a line having specified end points. There can be infinite number of line segments on a line. In the following diagram, AB is a denoted line segment. Two line segments having equal length are called congruent line segments.  Types of Lines:
Types of Lines:
- Horizontal Lines are parallel to the x-axis of the two dimensional plane

- Vertical Lines are parallel to the y-axis of the two-dimensional plane
- Parallel Lines – If the distance between two straight lines remain same throughout their length at all points, they are said to be parallel. In other words, they do not intersect anywhere in the plane.

- Perpendicular Lines – If a horizontal and vertical line intersect each other on a plane, they are perpendicular.
Angles: When two straight lines intersect at a point, they are said to form an angle. It can be measured in degree or radian. The straight lines are called arms of the angle and the point of intersection is called vertex.  Types of Angles:
Types of Angles:
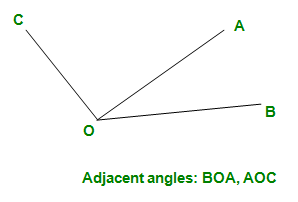
- Adjacent Angles – Angles which lie on either side of a common arm. In the following figure, angles BOA and AOC are adjacent having a common arm OA
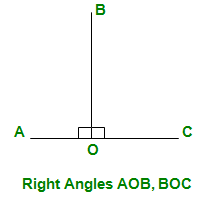
- Right Angle – When the adjacent angles are equal to each other for two intersecting lines, each of the angle is called right angle, denoted by 90o (represented as a small square)
- Acute Angle – An angle which is less than one right angle (less than 90o) is called acute angle
- Obtuse Angle – An angle which is greater than one right angle (greater than 90o) is called obtuse angle
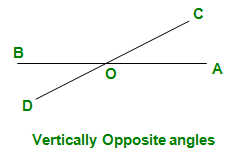
- Vertically Opposite Angles – When two straight lines intersect and cross each other at O, the angles AOC and DOB are vertically opposite. Angles DOA and BOC are also vertically opposite to each other. Further, these angles have equal measure (congruent angles)
- Reflex Angle – An angle which is greater than two right angles but less than four right angles is said to be reflex
- Supplementary Angles – Two angles whose sum is two right angles are said to be supplementary
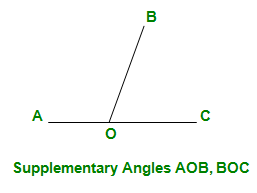
- Complementary Angles – Two angles whose sum is one right angle are said to be complementary
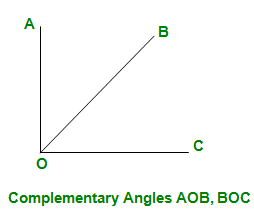
Angle bisector – If two adjacent angles are equal, then the line segment arm common to both the angles is known as the angle bisector. 
Examples: Example-1: In the figure shown below, it is given that angle BOC is a right angle and angle JHC is 30o. Further, lines AJ and DI are parallel. Find the value of angle OFG.  Solution – Firstly, angles JHC and angle GHE are vertically opposite. Hence,
Solution – Firstly, angles JHC and angle GHE are vertically opposite. Hence,
angle JHC = angle GHE
=> angle GHE = 30o
Now, lines AJ and DI are parallel; and angles GHE and FGH are supplementary.
=> angle GHE + angle FGH = 180o
=> angle FGH = 180o - angle GHE
=> angle FGH = 180o - 30o
=> angle FGH = 150o
Again, angles FGH and angle OGF are supplementary to each other
=> angle FGH + angle OGF = 180o
=> angle OGF = 180o - angle FGH
=> angle OGF = 180o - 150o
=> angle OGF = 30o
Finally, it is given angle FOG = 90o, hence angles OGF and OFG are complementary.
So angle OGF + angle OFG = 90o
=> angle OFG = 90o - angle OGF
=> angle OFG = 90o - 30o
=> angle OFG = 60o
Therefore, the desired angle OFG
= 60o
Example-2: In the figure shown below, if x = y + 30o, and AB is parallel to CD. Find the value of angle y.  Solution – Applying the concept of vertical angles, it is understood that,
Solution – Applying the concept of vertical angles, it is understood that,
angle Dxy = angle x
Now angles x and y are supplementary,
Hence, angle x + angle y = 180o
=> (angle y + 30o) + angle y = 180o
=> 2 * angle y = 180o - 30o
=> angle y = 150o/2
=> angle y = 75o
Therefore, the desired angle y is 75o
Share your thoughts in the comments
Please Login to comment...