GRE Geometry | Polygons
Last Updated :
18 Apr, 2019
Polygons:
The word polygon is derived from the Greek word polugonon, here poly means many and gons means angles. Polygons can be defined as a closed curve made up of line segments. Each line segment will become sides of the polygon.
Classification of polygons:
On the basis of the number of sides polygons are classified as follows:
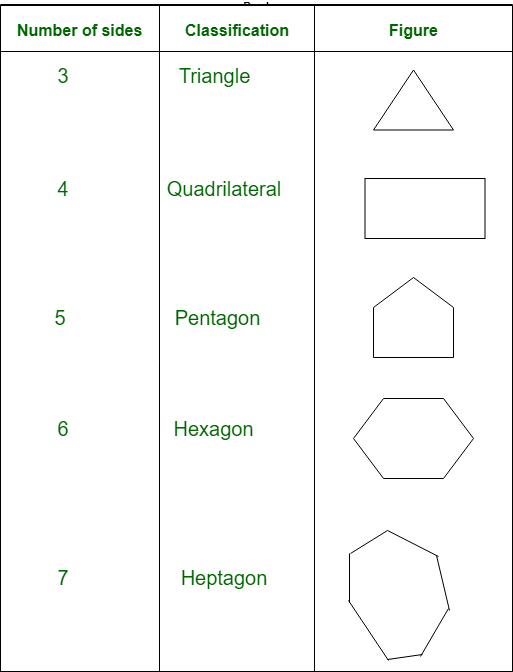
For n sides, we can call it n-gon. From here we can observe that the triangle is a polygon with least number of sides.
Concave and Convex polygon:
Convex polygons are the polygons whose all diagonal lie inside the figure and Concave polygons are those whose any diagonal lie outside the figure.

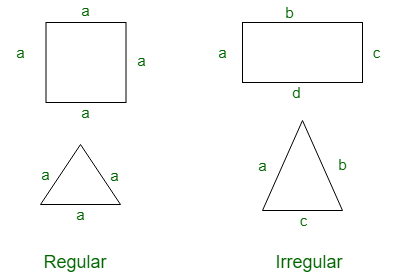
Regular and Irregular polygon:
Regular polygons are the polygons having all sides of equal length and Irregular polygons are the polygons having different side length.
Note:
- For a polygon, Exterior angle + Interior angle = 360°
- The sum of all exterior angles of polygon is 360°
- In a regular polygon all interior angles are equal.
- In a regular polygon all exterior angles are also equal.
- For a regular polygon, Number of sides = 360/exterior angle.
- Sum of all interior angles of a polygon is given by (n-2)*180, where ‘n’ is the number of sides in the polygon.
- Area of a polygon means area enclosed by the polygon and Perimeter of a polygon is sum of all the side length.
Examples:
- Example-1: What is the sum of all interior angles of heptagon ?
Solution:
Since it is a Heptagon, number of sides (n) = 7
Sum of all interior angles = (n-1)*180
So, for heptagon sum of interior angles = (7-2)*180 = 900
- Example-2: Calculate the number of side in a regular polygon having exterior angle 45° ?
Solution:
Number of sides = 360/exterior angle
Since exterior angle is 45°
number of sides = 360/45 = 8
- Example-3: What will be the value of an interior angle for a regular hexagon?
Solution:
Since it is a hexagon, number of sides (n) = 6
exterior angle = 360°/6 = 60
we know that, interior angle + exterior angle = 180°
interior angle + 60° = 180°
interior angle = 180° - 60°
interior angle = 120 °
- Example-4: Exterior angle of a regular polygon is 8°.
(a) find the number of sides in the polygon?
(b) find the interior angle of the polygon?
Solution:
(a) Number of sides = 360°/8°= 45
(b) interior angle = 180°- 8° = 172
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...