Find two disjoint good sets of vertices in a given graph
Given an undirected unweighted graph with N vertices and M edges. The task is to find two disjoint good sets of vertices. A set X is called good if for every edge UV in the graph at least one of the endpoint belongs to X(i.e, U or V or both U and V belongs to X).
If it is not possible to make such sets then print -1.
Examples:
Input :
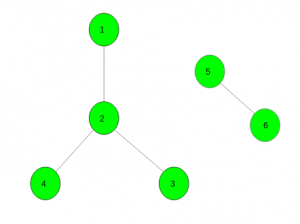
Output : {1 3 4 5} ,{2 6}
One disjoint good set contains vertices {1, 3, 4, 5} and other contains {2, 6}.
Input :
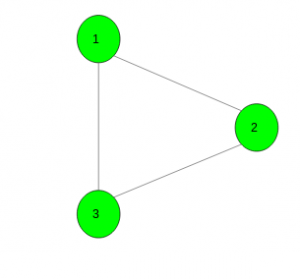
Output : -1
Approach:
One of the observation is that there is no edge UV that U and V are in the same set.The two good sets form a bipartition of the graph, so the graph has to be bipartite. And being bipartite is also sufficient. Read about bipartition here.
Below is the implementation of the above approach :
C++
// C++ program to find two disjoint// good sets of vertices in a given graph#include <bits/stdc++.h>using namespace std;#define N 100005// For the graphvector<int> gr[N], dis[2];bool vis[N];int colour[N];bool bip;// Function to add edgevoid Add_edge(int x, int y){ gr[x].push_back(y); gr[y].push_back(x);}// Bipartie functionvoid dfs(int x, int col){ vis[x] = true; colour[x] = col; // Check for child vertices for (auto i : gr[x]) { // If it is not visited if (!vis[i]) dfs(i, col ^ 1); // If it is already visited else if (colour[i] == col) bip = false; }}// Function to find two disjoint// good sets of vertices in a given graphvoid goodsets(int n){ // Initially assume that graph is bipartie bip = true; // For every unvisited vertex call dfs for (int i = 1; i <= n; i++) if (!vis[i]) dfs(i, 0); // If graph is not bipartie if (!bip) cout << -1; else { // Differentiate two sets for (int i = 1; i <= n; i++) dis[colour[i]].push_back(i); // Print vertices belongs to both sets for (int i = 0; i < 2; i++) { for (int j = 0; j < dis[i].size(); j++) cout << dis[i][j] << " "; cout << endl; } }}// Driver codeint main(){ int n = 6, m = 4; // Add edges Add_edge(1, 2); Add_edge(2, 3); Add_edge(2, 4); Add_edge(5, 6); // Function call goodsets(n);} |
Java
// Java program to find two disjoint// good sets of vertices in a given graphimport java.util.*;class GFG{ static int N = 100005; // For the graph @SuppressWarnings("unchecked") static Vector<Integer>[] gr = new Vector[N], dis = new Vector[2]; static { for (int i = 0; i < N; i++) gr[i] = new Vector<>(); for (int i = 0; i < 2; i++) dis[i] = new Vector<>(); } static boolean[] vis = new boolean[N]; static int[] color = new int[N]; static boolean bip; // Function to add edge static void add_edge(int x, int y) { gr[x].add(y); gr[y].add(x); } // Bipartie function static void dfs(int x, int col) { vis[x] = true; color[x] = col; // Check for child vertices for (int i : gr[x]) { // If it is not visited if (!vis[i]) dfs(i, col ^ 1); // If it is already visited else if (color[i] == col) bip = false; } } // Function to find two disjoint // good sets of vertices in a given graph static void goodsets(int n) { // Initially assume that graph is bipartie bip = true; // For every unvisited vertex call dfs for (int i = 1; i <= n; i++) if (!vis[i]) dfs(i, 0); // If graph is not bipartie if (!bip) System.out.println(-1); else { // Differentiate two sets for (int i = 1; i <= n; i++) dis[color[i]].add(i); // Print vertices belongs to both sets for (int i = 0; i < 2; i++) { for (int j = 0; j < dis[i].size(); j++) System.out.print(dis[i].elementAt(j) + " "); System.out.println(); } } } // Driver Code public static void main(String[] args) { int n = 6, m = 4; // Add edges add_edge(1, 2); add_edge(2, 3); add_edge(2, 4); add_edge(5, 6); // Function call goodsets(n); }}// This code is contributed by// sanjeev2552 |
Python 3
# Python 3 program to find two disjoint# good sets of vertices in a given graphN = 100005# For the graphgr = [[] for i in range(N)]dis = [[] for i in range(2)]vis = [False for i in range(N)]colour = [0 for i in range(N)]bip = 0# Function to add edgedef Add_edge(x, y): gr[x].append(y) gr[y].append(x)# Bipartie functiondef dfs(x, col): vis[x] = True colour[x] = col # Check for child vertices for i in gr[x]: # If it is not visited if (vis[i] == False): dfs(i, col ^ 1) # If it is already visited elif (colour[i] == col): bip = False# Function to find two disjoint# good sets of vertices in a given graphdef goodsets(n): # Initially assume that # graph is bipartie bip = True # For every unvisited vertex call dfs for i in range(1, n + 1, 1): if (vis[i] == False): dfs(i, 0) # If graph is not bipartie if (bip == 0): print(-1) else: # Differentiate two sets for i in range(1, n + 1, 1): dis[colour[i]].append(i) # Print vertices belongs to both sets for i in range(2): for j in range(len(dis[i])): print(dis[i][j], end = " ") print('\n', end = "")# Driver codeif __name__ == '__main__': n = 6 m = 4 # Add edges Add_edge(1, 2) Add_edge(2, 3) Add_edge(2, 4) Add_edge(5, 6) # Function call goodsets(n)# This code is contributed# by Surendra_Gangwar |
C#
// C# program to find two// disjoint good sets of// vertices in a given graphusing System;using System.Collections.Generic;class GFG{static int N = 100005;// For the graphstatic List<int>[] gr = new List<int>[N], dis = new List<int>[2]; static bool[] vis = new bool[N];static int[] color = new int[N];static bool bip;// Function to add edgestatic void add_edge(int x, int y){ gr[x].Add(y); gr[y].Add(x);}// Bipartie functionstatic void dfs(int x, int col){ vis[x] = true; color[x] = col; // Check for child vertices foreach (int i in gr[x]) { // If it is not visited if (!vis[i]) dfs(i, col ^ 1); // If it is already visited else if (color[i] == col) bip = false; }}// Function to find two disjoint// good sets of vertices in a// given graphstatic void goodsets(int n){ // Initially assume that // graph is bipartie bip = true; // For every unvisited // vertex call dfs for (int i = 1; i <= n; i++) if (!vis[i]) dfs(i, 0); // If graph is not bipartie if (!bip) Console.WriteLine(-1); else { // Differentiate two sets for (int i = 1; i <= n; i++) dis[color[i]].Add(i); // Print vertices belongs // to both sets for (int i = 0; i < 2; i++) { for (int j = 0; j < dis[i].Count; j++) Console.Write(dis[i][j] + " "); Console.WriteLine(); } }}// Driver Codepublic static void Main(String[] args){ int n = 6, m = 4; for (int i = 0; i < N; i++) gr[i] = new List<int>(); for (int i = 0; i < 2; i++) dis[i] = new List<int>(); // Add edges add_edge(1, 2); add_edge(2, 3); add_edge(2, 4); add_edge(5, 6); // Function call goodsets(n);}}// This code is contributed by shikhasingrajput |
Output:
1 3 4 5 2 6
Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.
In case you wish to attend live classes with industry experts, please refer Geeks Classes Live
