GFact | Why is Floating Point Arithmetic a problem in computing?

Have you ever tried to work with Floating Point Arithmetic in Computing? If yes, then have you ever tried to do 0.1 + 0.2 == 0.3 or some other operation on the precision of Floating point numbers? Yes, you guessed it right, the above expression evaluates to False even though it is mathematically correct. It seems like Floating-Point Arithmetic is broken, but is it so?

In this post, we will deep dive into the Precision and Rounding Errors of Floating Point Arithmetic, explain and justify floating point inaccuracies, and help you understand why “Floating Point Arithmetic is NOT BROKEN”.

What are the Inaccuracies in Floating Point Arithmetic?

To highlight the Inaccuracies in Floating Point Arithmetic, let us first understand couple of scenarios in computing:

Scenario 1: Let us try to evaluate 0.1 + 0.2 == 0.3

Consider the following code:

C++

#include <bits/stdc++.h>
using namespace std;

int main()
{

    // Evaluating a Floating Point
    // Arithmetic expression
    cout << "Evaluating if (0.1 + 0.2) equals 0.3 : ";
    if ((0.1 + 0.2) == 0.3) {
        cout << "Equal" << endl;
    }
    else {
        cout << "Not Equal" << endl;
    }

    return 0;
}

As you can see in the code above, we are just trying to evaluate if (0.1 + 0.2) equals (0.3) or not.

Expected Output:

Evaluating if (0.1 + 0.2) equals 0.3 : Equal

Actual Output:

Evaluating if (0.1 + 0.2) equals 0.3 : Not Equal

Scenario 2: Let us try Initialize a Floating Point Number to some specific Decimal Digits

Consider the following code:

C++

#include <bits/stdc++.h>
using namespace std;

int main()
{

    // Initialising a Floating Point number
    float x = 0.1;

    // Setting the count of Decimal Digits
    // to 18 digits and print the number
    cout << "Floating Point number 0.1 "
            "to 18 decimal digits: "
         << fixed << setprecision(18) << x << endl;

    return 0;
}

As you can see in the code above, when we initialize any floating point number then there might be some inaccuracy in its precision.

Expected Output:

Floating Point number 0.1 to 18 decimal digits: 0.100000000000000000

Actual Output:

Floating Point number 0.1 to 18 decimal digits: 0.100000001490116119

What is the Reason behind the Inaccuracies in Floating Point Arithmetic?

In most programming languages, Floating Point Arithmetic is based on the IEEE 754 standard.

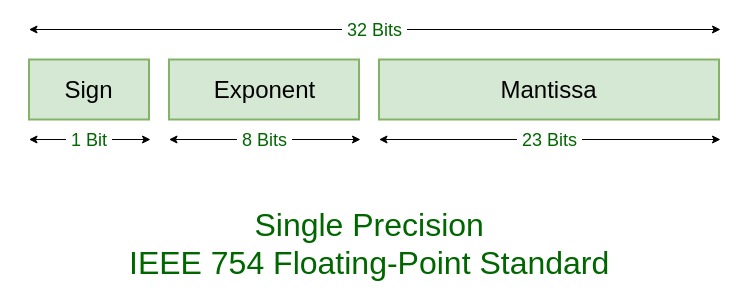
The crux of the problem is that Floating-point representations have a base b (which is always assumed to be even) and a precision p, where b and p are always a whole number.

Example: Let us try to store 0.1 in two bases – base 10 and base 2

• If b = 10 and p = 3, then the number 0.1 is stored as follows:

0.1 = 1/10, so

• numerator 1 will be represented in 3 digits (precision p) as 1.00
• denominator 10 will be represented in the exponential form of base 10 (b) as 10^-1

Therefore, 0.1 is represented as 1.00 × 10^-1.

• If b = 2 and p = 24, then the number 0.1 is stored as follows:

0.1 = 1/10, so

• numerator 1 will be represented in 24 digits (precision p) as 1.10011001100110011001101
• denominator 10 cannot be represented exactly in the exponential form of base 2 (b). So instead an approximation value is used by Rounding off to the base 2 as 2^-4

Therefore, 0.1 is represented approximately as 1.10011001100110011001101 × 2^-4.

As a result of these approximations, Floating Point Arithmetic results in following errors:

• Rounding Errors
• Precision Errors
• Relative Error and Ulps
• Guard Digits, etc.

How did the Inaccuracies in Floating Point Arithmetic resulted in the above deviations in Output?

Scenario 1: Let us try to evaluate 0.1 + 0.2 == 0.3

The constants 0.2 and 0.3 in your program will also be approximations to their true values. It happens that the closest double to 0.2 is larger than the rational number 0.2 but that the closest double to 0.3 is smaller than the rational number 0.3 , the sum of 0.1 and 0.2 winds up being larger than the rational number 0.3 and hence disagreeing with the constant in your code.

Scenario 2: Let us try Initialize a Floating Point Number to some specific Decimal Digits

For 0.1 in the standard binary64 format:

The representation can be written exactly as

• 0.1 in decimal ,or
• 0.1000000000000000055511151231257827021181583404541015625 in binary64, or
• 0x1.999999999999ap-4 in C99 hex float notation.

So the answer is “NO binary floating point numbers are not broken, they just happen to be as imperfect as every other base-N number system“.

How to Avoid the Inaccuracies in Floating Point Arithmetic?

• This problem of precision means you need to use rounding functions, to round your floating point numbers off to however many decimal places you’re interested in, before dispaying them.
• You also need to replace equality tests with comparisons that allow some amount of tolerance, which means:

• Do not do: if (x == y) { … }
• Instead do: if (abs(x – y) < myToleranceValue) { … },
  where
  • abs is the absolute value.
  • myToleranceValue needs to be chosen for your particular application, and it will have a lot to do with how much “wiggle room” you are prepared to allow, and what the largest number you are going to be comparing may be (due to loss of precision issues).

• Beware of “epsilon” style constants in your language of choice. These can be used as tolerance values but their effectiveness depends on the magnitude (size) of the numbers you’re working with, since calculations with large numbers may exceed the epsilon threshold.

Reference: What Every Computer Scientist Should Know About Floating-Point Arithmetic