IEEE Standard 754 Floating Point Numbers

The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point computation which was established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating point implementations that made them difficult to use reliably and reduced their portability. IEEE Standard 754 floating point is the most common representation today for real numbers on computers, including Intel-based PC’s, Macs, and most Unix platforms.

There are several ways to represent floating point number but IEEE 754 is the most efficient in most cases. IEEE 754 has 3 basic components:

1. The Sign of Mantissa –
   This is as simple as the name. 0 represents a positive number while 1 represents a negative number.
2. The Biased exponent –
   The exponent field needs to represent both positive and negative exponents. A bias is added to the actual exponent in order to get the stored exponent.
3. The Normalised Mantissa –
   The mantissa is part of a number in scientific notation or a floating-point number, consisting of its significant digits. Here we have only 2 digits, i.e. O and 1. So a normalised mantissa is one with only one 1 to the left of the decimal.

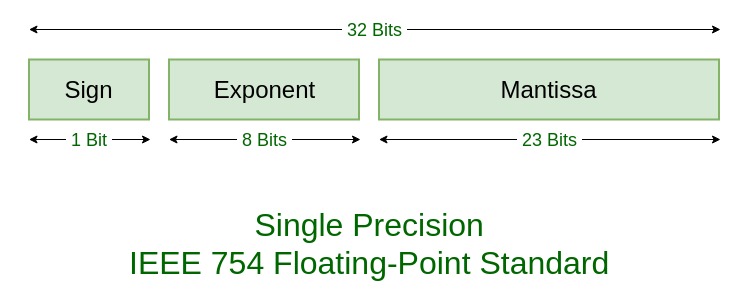
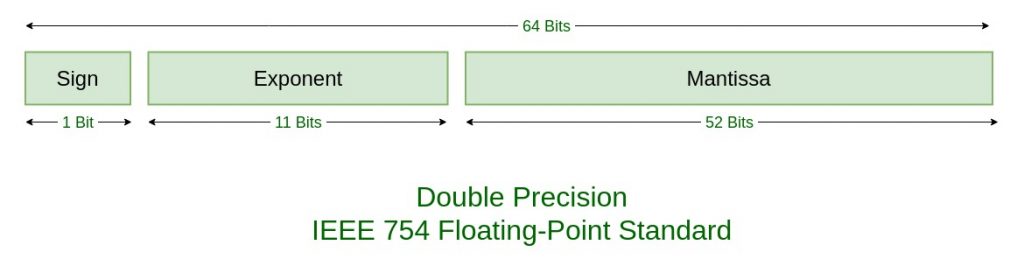
IEEE 754 numbers are divided into two based on the above three components: single precision and double precision.

TYPES	SIGN	BIASED EXPONENT	NORMALISED MANTISA	BIAS
Single precision	1(31st bit)	8(30-23)	23(22-0)	127
Double precision	1(63rd bit)	11(62-52)	52(51-0)	1023

Example –

85.125
85 = 1010101
0.125 = 001
85.125 = 1010101.001
       =1.010101001 x 2^6 
sign = 0 

1. Single precision:
biased exponent 127+6=133
133 = 10000101
Normalised mantisa = 010101001
we will add 0's to complete the 23 bits

The IEEE 754 Single precision is:
= 0 10000101 01010100100000000000000
This can be written in hexadecimal form 42AA4000

2. Double precision:
biased exponent 1023+6=1029
1029 = 10000000101
Normalised mantisa = 010101001
we will add 0's to complete the 52 bits

The IEEE 754 Double precision is:
= 0 10000000101 0101010010000000000000000000000000000000000000000000
This can be written in hexadecimal form 4055480000000000 

Special Values: IEEE has reserved some values that can ambiguity.

• Zero –
  Zero is a special value denoted with an exponent and mantissa of 0. -0 and +0 are distinct values, though they both are equal.
• Denormalised –
  If the exponent is all zeros, but the mantissa is not then the value is a denormalized number. This means this number does not have an assumed leading one before the binary point.
• Infinity –
  The values +infinity and -infinity are denoted with an exponent of all ones and a mantissa of all zeros. The sign bit distinguishes between negative infinity and positive infinity. Operations with infinite values are well defined in IEEE.
• Not A Number (NAN) –
  The value NAN is used to represent a value that is an error. This is represented when exponent field is all ones with a zero sign bit or a mantissa that it not 1 followed by zeros. This is a special value that might be used to denote a variable that doesn’t yet hold a value.

EXPONENT	MANTISA	VALUE
0	0	exact 0
255	0	Infinity
0	not 0	denormalised
255	not 0	Not a number (NAN)

Similar for Double precision (just replacing 255 by 2049), Ranges of Floating point numbers:

	Denormalized	Normalized	Approximate Decimal
Single Precision	± 2-149 to (1 – 2-23)×2-126	± 2-126 to (2 – 2-23)×2127	± approximately 10-44.85 to approximately 1038.53
Double Precision	± 2-1074 to (1 – 2-52)×2-1022	± 2-1022 to (2 – 2-52)×21023	± approximately 10-323.3 to approximately 10308.3

The range of positive floating point numbers can be split into normalized numbers, and denormalized numbers which use only a portion of the fractions’s precision. Since every floating-point number has a corresponding, negated value, the ranges above are symmetric around zero.

There are five distinct numerical ranges that single-precision floating-point numbers are not able to represent with the scheme presented so far:

1. Negative numbers less than – (2 – 2^-23) × 2¹²⁷ (negative overflow)
2. Negative numbers greater than – 2^-149 (negative underflow)
3. Zero
4. Positive numbers less than 2^-149 (positive underflow)
5. Positive numbers greater than (2 – 2^-23) × 2¹²⁷ (positive overflow)

Overflow generally means that values have grown too large to be represented. Underflow is a less serious problem because is just denotes a loss of precision, which is guaranteed to be closely approximated by zero.

Table of the total effective range of finite IEEE floating-point numbers is shown below:

	Binary	Decimal
Single	± (2 – 2-23) × 2127	approximately ± 1038.53
Double	± (2 – 2-52) × 21023	approximately ± 10308.25

Special Operations –

Operation	Result
n ÷ ±Infinity	0
±Infinity × ±Infinity	±Infinity
±nonZero ÷ ±0	±Infinity
±finite × ±Infinity	±Infinity
Infinity + Infinity Infinity – -Infinity	+Infinity
-Infinity – Infinity -Infinity + – Infinity	– Infinity
±0 ÷ ±0	NaN
±Infinity ÷ ±Infinity	NaN
±Infinity × 0	NaN
NaN == NaN	False